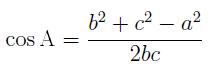Справочник по математике Геометрия (Планиметрия)
Геометрия (Планиметрия) Треугольники
Треугольники
Теорема Пифагора. Теорема косинусов
Содержание
 |
Теорема Пифагора |
 |
Теорема косинусов |

Теорема Пифагора
ТЕОРЕМА ПИФАГОРА. В прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы.
ДОКАЗАТЕЛЬСТВО. Докажем, что длины сторон произвольного прямоугольного треугольника ABC (рис.1)
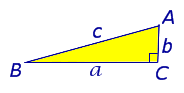
Рис.1
удовлетворяют равенству
c2 = a2 + b2
С этой целью рассмотрим квадрат со стороной, равной c, изображённый на рисунке 2.
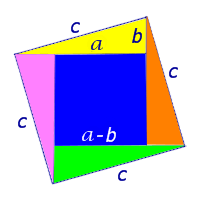
Рис.2
Площадь этого квадрата равна сумме площадей четырёх одинаковых прямоугольных треугольников, равных треугольнику ABC, и площади квадрата со стороной, равной a – b (рис.3).
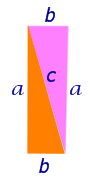
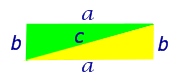
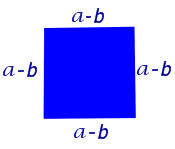
Рис.3
Поэтому справедливо равенство
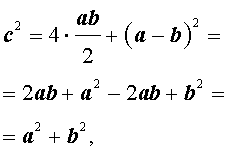
что и требовалось доказать.
Теорема косинусов
ТЕОРЕМА КОСИНУСОВ. Квадрат длины стороны треугольника равен сумме квадратов длин других сторон минус удвоенное произведение длин этих сторон на косинус угла между ними.
ДОКАЗАТЕЛЬСТВО. Рассмотрим сначала треугольник ABC, у которого углы A и С – острые (рис.4).
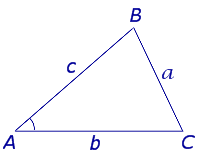
Рис.4
Докажем, что длины сторон этого треугольника удовлетворяют равенству
| a2 = b 2 + c 2 – 2bc cos A | (1) |
С этой целью проведём высоту BD из вершины B (рис.5).
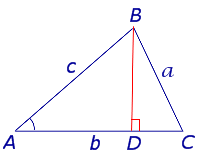
Рис.5
В соответствии с определениями синуса и косинуса угла прямоугольного треугольника справедливы равенства
BD = c sin A, AD = c cos A, DC = b – AD = b – c cos A.
Из теоремы Пифагора, применённой к прямоугольному треугольнику BDC, получим
a 2 = BD 2 + DC 2 =
= c 2 sin2 A + (b – c cos A)2 =
= c 2 sin2 A + b2 – 2 bc cos A + c 2 cos2 A =
= b2 + c 2 – 2 bc cos A.
Таким образом, в случае треугольника ABC с острыми углами A и С теорема косинусов доказана.
ЗАМЕЧАНИЕ 1. Для того, чтобы получить полное доказательство теоремы косинусов, необходимо рассмотреть также и следующие случаи:
- Угол A – острый, угол C – тупой (рис.6)
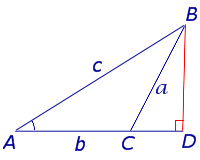
Рис.6
- Угол A – прямой (рис. 7).
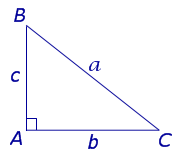
Рис.7
- Угол A – тупой (рис.8).
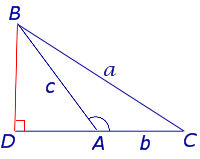
Рис.8
Во всех перечисленных случаях доказательства теоремы косинусов проводятся совершенно аналогично тому, как это было сделано для случая острых углов A и C, и мы рекомендуем читателю провести эти доказательства в качестве полезного и несложного упражнения.
ЗАМЕЧАНИЕ 2. В случае, когда угол A является прямым углом, формула (1) принимает вид
a2 = b2 + c2,
откуда вытекает, что теорема Пифагора является частным случаем теоремы косинусов.
ЗАМЕЧАНИЕ 3. Если у треугольника известны длины всех сторон, то с помощью теоремы косинусов можно найти косинус любого угла треугольника, например,