Справочник по математике Геометрия (Планиметрия)
Геометрия (Планиметрия) Четырехугольники
Четырехугольники
Параллелограммы
Содержание
 |
Свойства и признаки параллелограмма |
 |
Свойства и признаки прямоугольника |
 |
Свойства и признаки ромба |
 |
Свойства и признаки квадрата |

Свойства и признаки параллелограмма
| Определение параллелограмма |
|
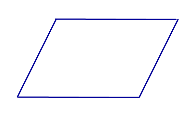
Определение Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны |
| Определение диагонали параллелограмма |
|
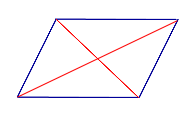
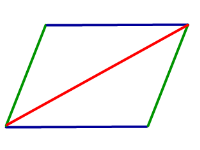
Определение Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины |
| Определение высоты параллелограмма |
|
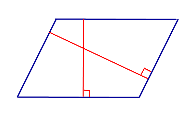
Определение Высотой параллелограмма называют перпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение |
| Свойство противолежащих сторон параллелограмма |
|
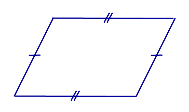
Свойство Если четырёхугольник является параллелограммом, то его противолежащие стороны равны. |
| Признак параллелограмма: равенство противолежащих сторон |
|
Признак Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом. |
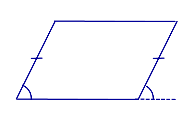
| Признак параллелограмма: равенство и параллельность двух противолежащих сторон |
|
Признак Если у четырёхугольника две противолежащие стороны равны и параллельны, то он является параллелограммом. |
| Свойство диагоналей параллелограмма |
|
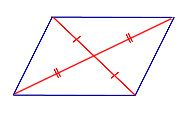
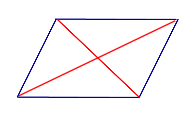
Свойство Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам. |
| Признак параллелограмма: диагонали точкой пересечения делятся пополам |
|
Признак Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом. |
| Свойство углов, прилежащих к сторонам параллелограмма |
|
Свойство Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180°. |
| Признак параллелограмма: суммы углов, прилежащих к сторонам |
|
Признак Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180°, то четырёхугольник является параллелограммом. |
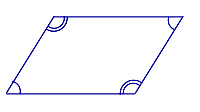
| Свойство противолежащих углов параллелограмма |
|
Свойство Если четырёхугольник является параллелограммом, то его противолежащие углы равны. |
| Признак параллелограмма: равенство противолежащих углов |
|
Признак Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом. |
| Свойство диагонали параллелограмма |
|
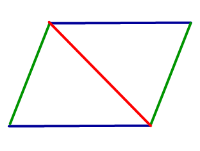
Свойство Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника. |
| Признак параллелограмма: равенство двух треугольников, на которые каждая диагональ делит четырёхугольник |
|
Признак Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом. |
| Свойство диагоналей параллелограмма |
|
Свойство Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника) |
| Признак параллелограмма: равенство площадей четырех треугольников, на которые диагонали делят четырёхугольник |
|
Признак Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом. |
Свойства и признаки прямоугольника
| Определение прямоугольника |
|
Определение Прямоугольником называют параллелограмм, у которого все углы прямые. |
| Свойство диагоналей прямоугольника |
|
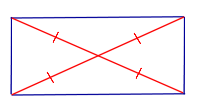
Свойство Если параллелограмм является прямоугольником, то его диагонали равны. |
| Признак прямоугольника: равенство диагоналей |
|
Признак Если у параллелограмма диагонали равны, то он является прямоугольником. |
Свойства и признаки ромба
| Определение ромба |
|
Определение Ромбом называют параллелограмм, у которого все стороны равны |
| Свойство диагоналей ромба |
|
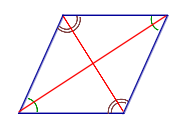
Свойство Если параллелограмм является ромбом, то его диагонали являются биссектрисами углов |
| Признак ромба: диагонали – биссектрисы углов |
|
Признак Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом |
| Свойство диагоналей ромба |
|
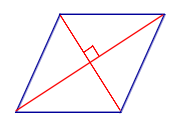
Свойство Если параллелограмм является ромбом, то его диагонали перпендикулярны |
| Признак ромба: перпендикулярность диагоналей |
|
Признак Если у параллелограмма диагонали перпендикулярны, то он является ромбом |
Свойства и признаки квадрата
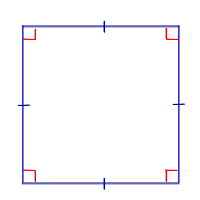
| Определение квадрата |
|
Определение Квадратом называют параллелограмм, у которого все стороны равны и все углы равны |
| Свойство диагоналей квадрата |
|
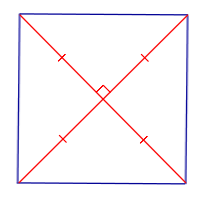
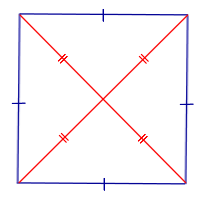
Свойство Если параллелограмм является квадратом, то его диагонали перпендикулярны и равны |
| Признак квадрата: равенство и перпендикулярность диагоналей |
|
Признак Если у параллелограмма диагонали перпендикулярны и равны, то он является квадратом |
| Свойство диагоналей квадрата |
|
Свойство Если прямоугольник является квадратом, то его диагонали перпендикулярны |
| Признак квадрата: перпендикулярность диагоналей |
|
Признак Если у прямоугольника диагонали перпендикулярны, то он является квадратом |
| Свойство диагоналей квадрата |
|
Свойство |
| Признак квадрата: равенство диагоналей |
|
Признак |