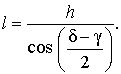Справочник по математике Геометрия (Планиметрия)
Геометрия (Планиметрия) Треугольники
Треугольники
Биссектриса треугольника
Напомним, что биссектрисой угла называют луч, делящий угол пополам.
ОПРЕДЕЛЕНИЕ. Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника и соединяющий вершину треугольника с точкой на противоположной стороне (рис 1).
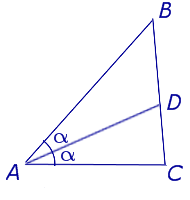
Рис.1
Поскольку в каждом треугольнике имеются три угла, то в каждом треугольнике можно провести три биссектрисы.
На рисунке 1 биссектрисой является отрезок AD.
ТЕОРЕМА 1 (свойство биссектрисы угла треугольника). Биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.
ДОКАЗАТЕЛЬСТВО. Продолжим сторону AC треугольника ABC, изображенного на рисунке 1, за точку A. Проведем через точку B прямую, параллельную биссектрисе AD. Обозначим точку пересечения построенных прямых буквой E (рис. 2).
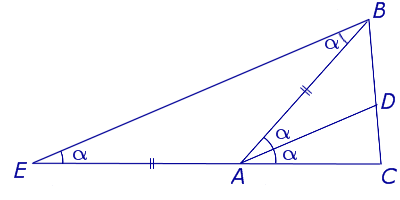
Рис.2
Докажем, что отрезки AB и AE равны. Для этого заметим, что угол EBA равен углу BAD, поскольку эти углы являются внутренними накрест лежащими при параллельных прямых EB и AD. Заметим также, что угол BEA равен углу DAC, поскольку эти углы являются соответственными при параллельных прямых EB и AD. Таким образом, угол EBA равен углу BEA, откуда вытекает, что треугольник EAB является равнобедренным, и отрезки AB и AE равны.
Отсюда, воспользовавшись теоремой Фалеса, получаем:

что и требовалось доказать.
СЛЕДСТВИЕ 1 (формулы для длин отрезков, на которые биссектриса угла треугольника делит противоположную сторону).
Рассмотрим рисунок 3, на котором изображен тот же треугольник, как и на рисунке 1, но для длин отрезков использованы обозначения
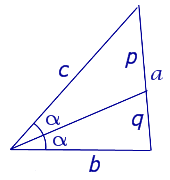
Рис.3
b = |AC|, a = |BC|, c = |AB|, p = |BD|, q = |DC|.
Тогда
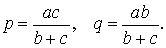
ДОКАЗАТЕЛЬСТВО. Поскольку
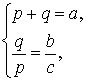
то
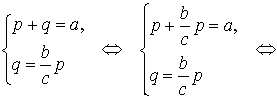
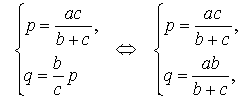
что и требовалось доказать.
СЛЕДСТВИЕ 2 (формулы для длин отрезков, на которые биссектрисы углов треугольника делятся в точке пересечения).
Рассмотрим рисунок 4, на котором изображены две биссектрисы треугольника, пересекающиеся в точке O.
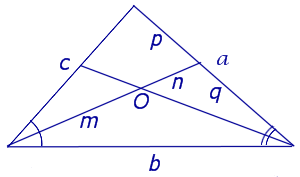
Рис.4
Тогда справедлива формула:
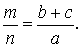
ДОКАЗАТЕЛЬСТВО. Поскольку
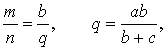
то
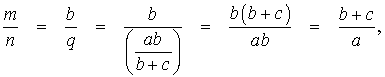
что и требовалось доказать.
ЗАМЕЧАНИЕ. В любом треугольнике все три биссектрисы пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.
ТЕОРЕМА 2 (формула, выражающая длину биссектрисы через две стороны и угол треугольника).
Рассмотрим рисунок 5, который практически совпадает с рисунком 2.
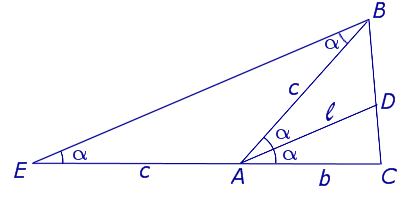
Рис.5
Тогда для длины биссектрисы справедлива формула:
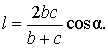
ДОКАЗАТЕЛЬСТВО. Из рисунка 5 следует формула
|EB| = 2c cos α .
Если воспользоваться этой формулой, то из подобия треугольников ADC и EBC, получаем:
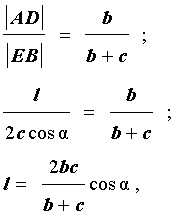
что и требовалось доказать.
ТЕОРЕМА 3 (формула, выражающая длину биссектрисы через стороны треугольника).
Длину биссектрисы треугольника (рис.6) можно найти по формуле:
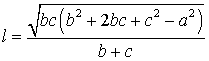
Доказательство. Рассмотрим рисунок 6
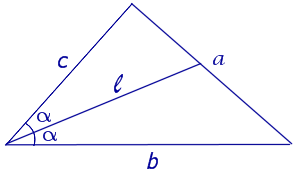
Рис.6
и воспользуемся теоремой косинусов:
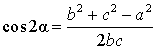
Теперь воспользуемся формулой «Косинус двойного угла»:
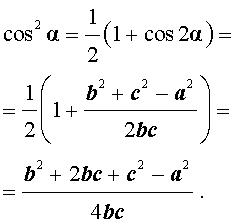
Следовательно,
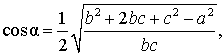
откуда с помощью Теоремы 2 получаем:
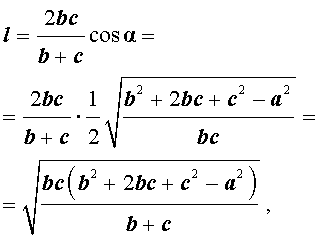
что и требовалось доказать.
ЗАДАЧА (формула для угла между биссектрисой и высотой, проведенных из одной вершины, через углы треугольника).
Из вершины C треугольника ABC (рис.7) проведена биссектриса CD и высота CE.
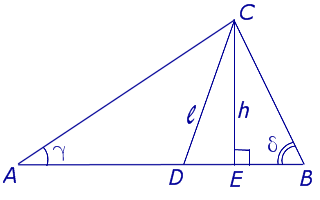
Рис.7
Доказать, что выполнено равенство:
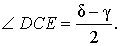
РЕШЕНИЕ. Поскольку CD – биссектриса угла ACB, то
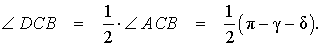
Поскольку CE – высота, то
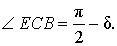
Следовательно,
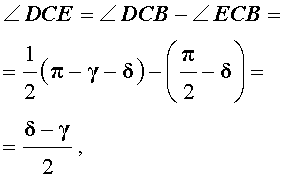
что и требовалось доказать.
Из решения этой задачи вытекает простое следствие.
СЛЕДСТВИЕ. Длины биссектрисы CD и высоты CE связаны формулой: