Справочник по математикеГеометрия (Планиметрия) Треугольники

Теорема Чевы

Содержание

	Теорема Чевы 1
	Теорема Чевы 2
	Применения теоремы Чевы

Теорема Чевы 1

ТЕОРЕМА ЧЕВЫ 1. Если на сторонах   AB, BC   и   CA   треугольника   ABC   взяты соответственно точки   C₁,   A₁   и   B₁   (рис.1), то отрезки    AA₁,   BB₁   и   CC₁   пересекаются в одной точке тогда и только тогда, когда выполнено равенство

(1)

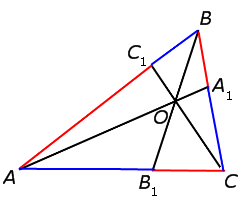
Рис.1

ДОКАЗАТЕЛЬСТВО НЕОБХОДИМОСТИ. Докажем, что, если отрезки   AA₁,   BB₁   и   CC₁   пересекаются в одной точке, то выполнено равенство (1). Для этого проведём через точку   B   прямую, параллельную прямой   AC ,   и обозначим буквами   D   и   C   точки пересечения прямых   CC₁   и   AA₁   с этой прямой соответственно (рис.2).

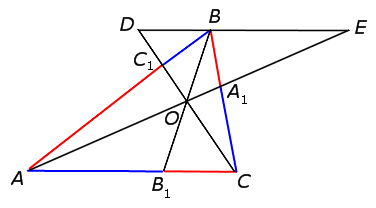
Рис.2

Поскольку треугольник   AC₁C   подобен треугольнику   DC₁B ,   то выполнено равенство

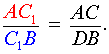(2)

Поскольку треугольник   AA₁C   подобен треугольнику   BA₁E ,   то выполнено равенство

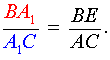(3)

Поскольку треугольник   CB₁O   подобен треугольнику   DBO ,   то выполнено равенство

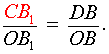(4)

Поскольку треугольник   AOB₁   подобен треугольнику   BOE ,   то выполнено равенство

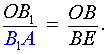(5)

Перемножая равенства (2 – 5), получим

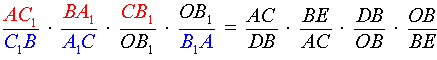
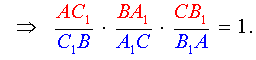
Доказательство необходимости завершено.

ДОКАЗАТЕЛЬСТВО ДОСТАТОЧНОСТИ. Докажем, что, если выполнено равенство (1), то отрезки   AA₁,  BB₁   и   CC₁   пересекаются в одной точке.

Воспользуемся методом «от противного». С этой целью обозначим буквой   O   точку пересечения отрезков   AA₁   и   CC₁   и предположим, что отрезок   BB₁   не проходит через точку   O   (рис. 3).

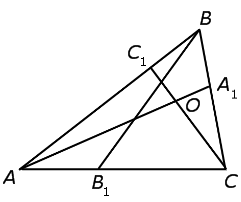
Рис.3

Проведём через точку   O   отрезок   BB₂   (рис. 4).

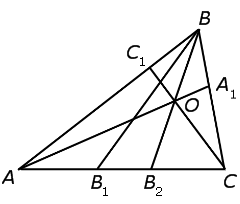
Рис.4

Поскольку отрезки   AA₁,  BB₂   и   CC₁   пересекаются в одной точке, то выполнено равенство

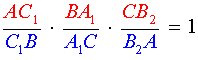(6)

Кроме того, выполнено равенство (1)

(1)

Разделив равенство (6) на равенство (1), получим равенство

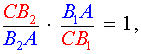
следствием которого является равенство

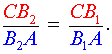(7)

Из равенства (7) вытекает, что точки   B₁   и   B₂   совпадают.

Доказательство достаточности завершено.

Теорема Чевы 2

ТЕОРЕМА ЧЕВЫ 2. Если на продолжениях за точку   B   сторон   AB   и   CB   треугольника   ABC   взяты соответственно точки   C₁, A₁ ,   а на стороне   CA   взята точка   B₁ ,   то прямые   AA₁ ,   BB₁   и   CC₁   пересекаются в одной точке или параллельны тогда и только тогда, когда выполнено равенство

(8)

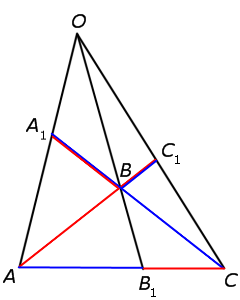
Рис.5

ДОКАЗАТЕЛЬСТВО НЕОБХОДИМОСТИ (случай «а»). Докажем, что, если прямые   AA₁,   BB₁   и   CC₁   пересекаются в одной точке (рис.5), то выполнено равенство (8). Для этого проведём через точку   B   прямую, параллельную прямой   AC ,   и обозначим буквами   D   и   C   точки пересечения прямых   AA₁   и   CC₁   с этой прямой соответственно (рис.6).

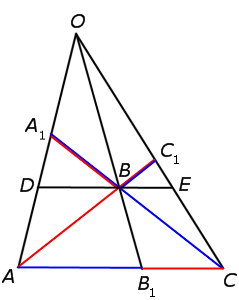
Рис.6

Поскольку треугольник   AС₁C   подобен треугольнику   BC₁E,   то выполнено равенство

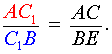(9)

Поскольку треугольник   AA₁C   подобен треугольнику   DA₁B,   то выполнено равенство

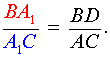(10)

Поскольку треугольник   ODB   подобен треугольнику   OAB₁,   то выполнено равенство

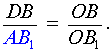(11)

Поскольку треугольник   BOE   подобен треугольнику   B₁OC,   то выполнено равенство

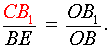(12)

Перемножая равенства (9 – 12), получим

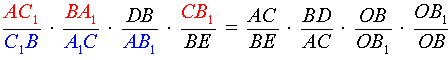
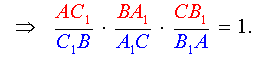
Доказательство необходимости в случае «а» завершено.

ДОКАЗАТЕЛЬСТВО НЕОБХОДИМОСТИ (случай «b»). Докажем, что если прямые   AA₁, BB₁   и   CC₁   параллельны (рис.7), то выполнено равенство (8).

Рис.7

Проведём через точку   B   прямую, параллельную прямой   AС,   и обозначим буквами   D   и   E   точки пересечения прямых   AA₁   и   CC₁   с этой прямой соответственно (рис.8).

Рис.8

Поскольку треугольник   AC₁C   подобен треугольнику   BC₁E,   то выполнено равенство

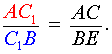(13)

Поскольку треугольник   AA₁C   подобен треугольнику   DA₁B,   то выполнено равенство

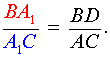(14)

Поскольку четырёхугольники   ADBB₁   и   BECB₁   параллелограммы, то выполнено равенство

CB₁ = BE,     B₁A = DB ,

откуда вытекает равенство

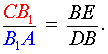(15)

Перемножая равенства (13 – 15), получим

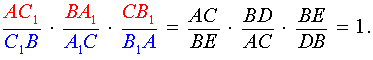
Доказательство необходимости в случае «b» завершено.

ЗАМЕЧАНИЕ. Доказательство достаточности условия (8) в случае 2 проводится аналогично тому, как это было сделано для случая 1, и мы оставляем его читателю в качестве упражнения.

Применения теоремы Чевы

В разделе нашего справочника «Медиана треугольника» доказана теорема о том, что медианы треугольника пересекаются в одной точке.

Приведём другое доказательство этой теоремы, основанное на теореме Чевы. С этой целью рассмотрим медианы   AA₁,  BB₁   и   CC₁   треугольника   ABC   (рис.9).

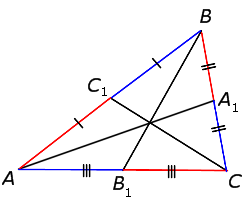
Рис.9

Поскольку

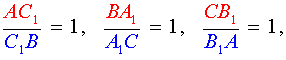
то выполнено равенство

,

откуда вытекает, что отрезки   AA₁,  BB₁   и   CC₁   пересекаются в одной точке.

Теорема доказана.

В разделе нашего справочника «Окружность, вписанная в треугольник» доказана теорема о том, что биссектрисы треугольника пересекаются в одной точке.

Приведём другое доказательство этой теоремы, основанное на теореме Чевы. С этой целью рассмотрим биссектрисы   AA₁,  BB₁   и   CC₁   треугольника   ABC   (рис.10).

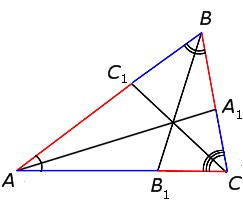
Рис.10

В соответствии со свойством биссектрисы справедливы равенства

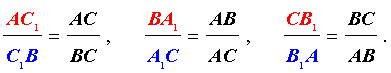
Если перемножить эти три равенства, то мы получим равенство

,

из которого вытекает, что отрезки AA₁,  BB₁ и CC₁пересекаются в одной точке.

Теорема доказана.

В разделе нашего справочника «Высота треугольника» доказана теорема о том, что высоты треугольника пересекаются в одной точке.

Приведём другое доказательство этой теоремы, основанное на теореме Чевы.

С этой целью рассмотрим сначала высоты   AA₁,  BB₁   и   CC₁   остроугольного треугольника   ABC   (рис.11).

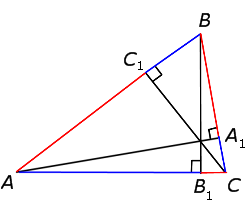
Рис.11

Поскольку

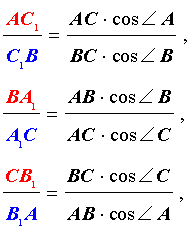
то, перемножив эти три равенства, мы получим равенство

,

из которого вытекает, что отрезки AA₁,  BB₁ и CC₁ пересекаются в одной точке.

Теорема о пересечении высот остроугольного треугольника доказана.

Теперь рассмотрим случай тупоугольного треугольника (рис. 12).

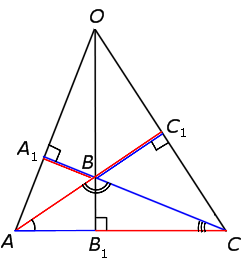
Рис.12

На рисунке 12 изображён треугольник   ABC   с тупым углом   B,   высотами которого являются отрезки   AA₁,  BB₁   и   CC₁.

Поскольку

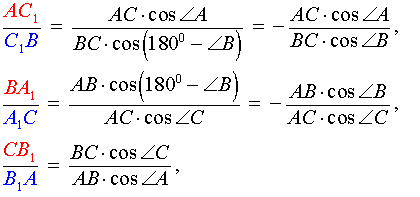
то, перемножив эти три равенства, мы получим равенство

,

из которого вытекает, что прямые   AA₁,  BB₁   и   CC₁   пересекаются в одной точке.

Теорема о пересечении высот тупоугольного треугольника доказана.

Доказывать теорему о том, что в случае прямоугольного треугольника все высоты пересекаются в одной точке не нужно, поскольку все высоты прямоугольного треугольника пересекаются в вершине прямого угла.

Теорема о пересечении высот треугольника доказана полностью.

Теперь с помощью теоремы Чевы докажем следующую теорему.

ТЕОРЕМА. Рассмотрим окружность, вписанную в произвольный треугольник   ABC.   Пусть точки   A₁,  B₁   и   C₁   – точки касания этой окружности со сторонами   BC, AC   и   AB   соответственно. Тогда отрезки   AA₁,  BB₁   и   CC₁   пересекаются в одной точке (рис. 13).

Рис.13

Доказательство. Воспользовавшись свойством равенства касательных, проведённых к окружности из одной точки, выпишем следующие равенства:

AC₁ = B₁A,       BA₁ = C₁B ,       CB₁ = A₁C.

      Из этих равенств получаем:

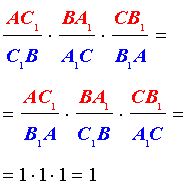
Отсюда с помощью теоремы Чевы заключаем, что отрезки   AA₁,  BB₁   и   CC₁   пересекаются в одной точке.

Теорема доказана.

ЗАМЕЧАНИЕ. Точку пересечения отрезков   AA₁,   BB₁   и   CC₁, о которых говорится в только что доказанной теореме, называют точкой Жергонна в честь французского математика Жозефа Жергонна (1771 г. – 1859 г.).