Справочник по математике Геометрия (Планиметрия)
Геометрия (Планиметрия) Окружность и круг
Окружность и круг
Две окружности на плоскости. Общие касательные к двум окружностям
Содержание
 |
Взаимное расположение двух окружностей |
 |
Общие касательные к двум окружностям |
 |
Формулы для длин общих касательных и общей хорды |
 |
Доказательства формул для длин общих касательных и общей хорды |

Взаимное расположение двух окружностей
| Взаимное расположение двух окружностей на плоскости |
|
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей |
| Каждая из окружностей лежит вне другой |
|
Расстояние между центрами окружностей больше суммы их радиусов d > r1 + r2 |
| Внешнее касание двух окружностей |
|
Расстояние между центрами окружностей равно сумме их радиусов d = r1 + r2 |
| Внутреннее касание двух окружностей |
|
Расстояние между центрами окружностей равно разности их радиусов d = r1 – r2 |
| Окружности пересекаются в двух точках |
|
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 < d < r1 + r2 |
| Одна из окружностей лежит внутри другой |
|
Расстояние между центрами окружностей меньше разности их радиусов d < r1 – r2 |
Общие касательные к двум окружностям
| Определение общей внешней касательной к двум окружностям |
|
Определение Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой. |
| Определение общей внутренней касательной к двум окружностям |
|
Определение Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой. |
| Случай внутреннего касания двух окружностей |
|
Существует единственная общая внешняя касательная. Других общих касательных нет. |
| Случай, когда окружности пересекаются в двух точках |
|
Существуют две общих внешних касательных. Других общих касательных нет. |
| Случай внешнего касания двух окружностей |
|
Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет. |
| Случай, когда каждая из окружностей лежит вне другой |
|
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет |
Формулы для длин общих касательных и общей хорды двух окружностей
| Формула для длины общей внешней касательной к двум окружностям |
|
Длина общей внешней касательной к двум окружностям вычисляется по формуле
|
| Формула для длины общей внутренней касательной к двум окружностям |
|
Длина общей внутренней касательной к двум окружностям вычисляется по формуле
|
| Формула для длины общей хорды двух окружностей |
|
Длина общей хорды двух окружностей вычисляется по формуле
|
Доказательства формул для длин общих касательных и общей хорды двух окружностей
УТВЕРЖДЕНИЕ 1. Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле

ДОКАЗАТЕЛЬСТВО. Для того, чтобы найти длину отрезка K1K2, опустим из точки O2 перпендикуляр O2K3 на прямую O1K1 (рис.1).

Рис.1
Поскольку четырёхугольник O2K2K1K3 – прямоугольник, то справедливы равенства
O2K3 = K1K2 , K1K3 = r2 , O1K3 = r1 – r2 .
Воспользовавшись этими равенствами, из прямоугольного треугольника O1O2K3 получаем:

Следовательно,

что и требовалось доказать.
УТВЕРЖДЕНИЕ 2. Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d, то длина общей внутренней касательной к этим окружностям вычисляется по формуле

ДОКАЗАТЕЛЬСТВО. Для того, чтобы найти длину отрезка K1K2 , опустим из точки O2 перпендикуляр O2K3 на прямую O1K1 (рис.2).

Рис.2
Поскольку четырёхугольник O2K2K1K3 – прямоугольник, то справедливы равенства
O2K3 = K1K3 , K1K3 = r2 , O1K3 = r1 + r2 .
Воспользовавшись этими равенствами, из прямоугольного треугольника O1O2K3 получаем:

Следовательно,

что и требовалось доказать.
УТВЕРЖДЕНИЕ 3. Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d, то длина общей хорды AB этих окружностей вычисляется по формуле

ДОКАЗАТЕЛЬСТВО. Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3,
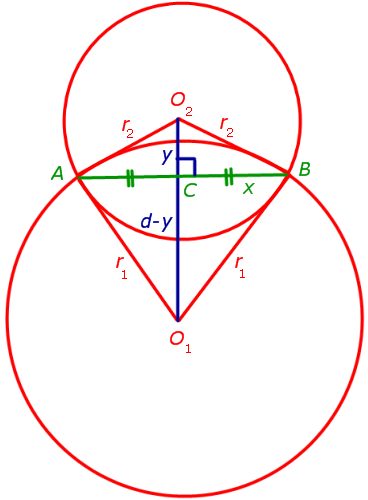
Рис.3
следующие обозначения:
O2C = y, CB = x .
Тогда, воспользовавшись теоремой Пифагора для треугольников O1CB и O2CB, получим
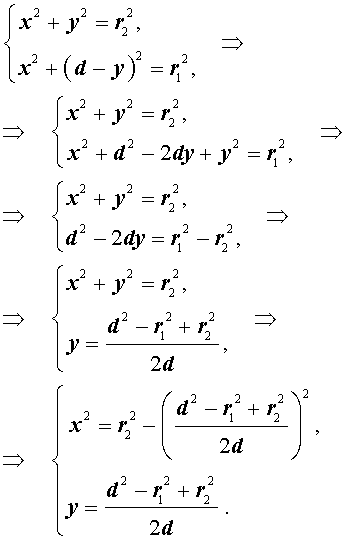
Поэтому
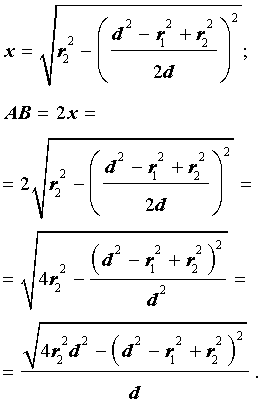
Таким образом, справедлива формула:

что и требовалось доказать.

















