Справочник по математике Геометрия (Планиметрия)
Геометрия (Планиметрия) Четырехугольники
Четырехугольники
Трапеции
Содержание
 |
Основные определения и свойства трапеций |
 |
Свойства и признаки равнобедренных трапеций |

Основные определения и свойства трапеций
| Определение трапеции |
|
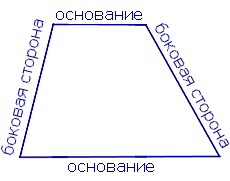
Определение Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции |
| Определение диагоналей трапеции |
|
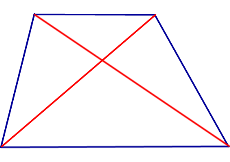
Определение Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции |
| Определение высоты трапеции |
|
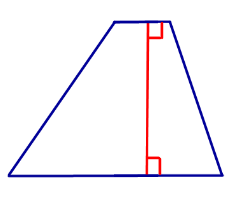
Определение Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение |
| Свойство точки пересечения диагоналей |
|
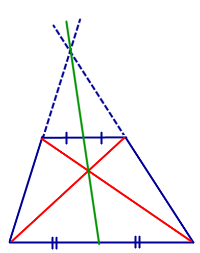
Свойство Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой |
| Определение средней линии трапеции |
|
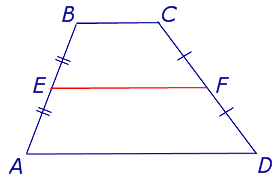
Определение Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции |
| Свойство средней линии трапеции |
|
Свойство Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме |
| Свойство биссектрис углов при боковой стороне трапеции |
|
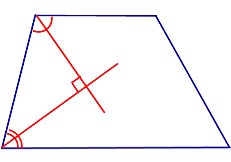
Свойство Биссектрисы углов при боковой стороне трапеции перпендикулярны |
Подробнее со свойствами средней линии трапеции можно ознакомиться в разделе нашего справочника «Средняя линия трапеции».
В разделе нашего справочника «Типы четырёхугольников» представлена схема классификации трапеций. В том же разделе представлена таблица, в которой описаны всевозможные типы трапеций.
Свойства и признаки равнобедренных трапеций
| Определение равнобедренной трапеции |
|
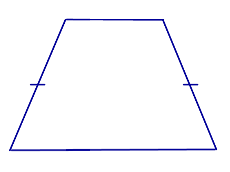
Определение Равнобедренной трапецией называют трапецию, у которой боковые стороны равны. |
| Свойство углов при основании равнобедренной трапеции |
|
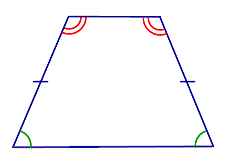
Свойство Если трапеция является равнобедренной, то углы при каждом из её оснований равны. |
| Признак равнобедренной трапеции: равенство углов при одном из оснований |
|
Признак Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной. |
| Свойство диагоналей равнобедренной трапеции |
|
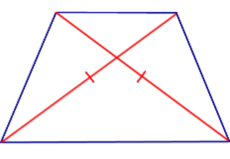
Свойство Если трапеция является равнобедренной, то её диагонали равны. |
| Признак равнобедренной трапеции: равенство диагоналей |
|
Признак Если у трапеции диагонали равны, то она является равнобедренной. |
| Свойство углов, которые диагонали образуют с основаниями равнобедренной трапеции |
|
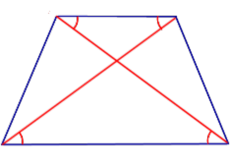
Свойство Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. |
| Признак равнобедренной трапеции: равные углы, которые образуют диагонали с одним из оснований равнобедренной трапеции |
|
Признак Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной. |
| Свойство равнобедренной трапеции |
|
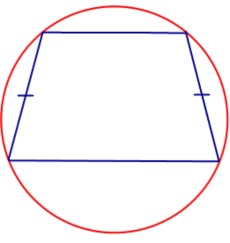
Свойство Если трапеция является равнобедренной, то около неё можно описать окружность. |
| Признак равнобедренной трапеции: существование окружности, описанной около равнобедренной трапеции |
|
Признак Если около трапеции можно описать окружность, то она является равнобедренной. |
| Свойство высот равнобедренной трапеции |
|
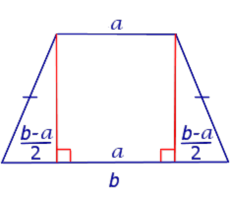
Свойство Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований |