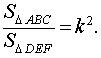Справочник по математике Геометрия (Планиметрия)
Геометрия (Планиметрия) Треугольники
Треугольники
Подобные треугольники. Признаки подобия треугольников
Содержание
 |
Подобные треугольники |
 |
Признаки подобия треугольников |
 |
Признаки подобия прямоугольных треугольников |

Подобные треугольники
Рассмотрим два треугольника KLM и TRP (рис.1) и введём следующие обозначения.
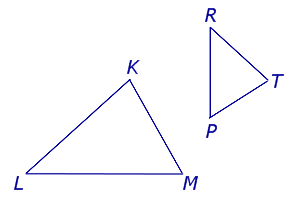
Рис.1
Обозначим
a1 , b1 , c1
длины сторон треугольника KLM, расположенные в порядке возрастания.
Обозначим
a2 , b2 , c2
длины сторон треугольника TRP, расположенные в порядке возрастания.
Переобозначим вершины треугольников KLM и TRP так, как показано на рисунке 2.
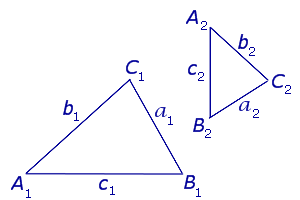
Рис.2
На рисунке 2 треугольник KLM обозначается как треугольник A1B1C1, а треугольник TRP обозначается как треугольник A2B2C2.
ОПРЕДЕЛЕНИЕ 1. В треугольниках A1B1C1 и A2B2C2, изображённых на рисунке 2,
 |
вершины A1 и A2, B1 и B2, C1 и C2 называют сходственными вершинами, |
 |
стороны A1B1 и A2B2, A1C1 и A2C2, B1C1 и B2C2 называют сходственными сторонами, |
 |
углы A1 и A2, B1 и B2, C1 и C2 называют сходственными углами |
ОПРЕДЕЛЕНИЕ 2. Треугольники A1B1C1 и A2B2C2 называют подобными треугольниками, если их сходственные углы равны, а сходственные стороны пропорциональны.
Другими словами, треугольники A1B1C1 и A2B2C2 подобны, если, во-первых,
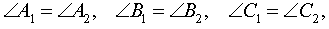
а, во-вторых, существует положительное число k, такое, что справедливы равенства:
| a1 = k a2 , b1 = k b2 , c1 = k c2 . | (1) |
ОПРЕДЕЛЕНИЕ 3. В случае, когда треугольники A1B1C1 и A2B2C2 подобны, число k, заданное формулами (1), называют коэффициентом подобия треугольников A1B1C1 и A2B2C2 .
Признаки подобия треугольников
| Признак подобия треугольников по двум сторонам и углу между ними |
|
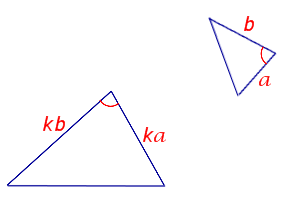
Формулировка признака подобия: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны.
|
| Признак подобия треугольников по двум углам |
|
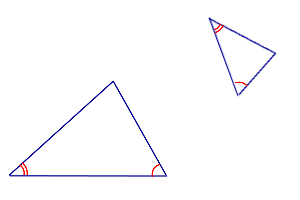
Формулировка признака подобия: Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
|
| Признак подобия треугольников по трём сторонам |
|
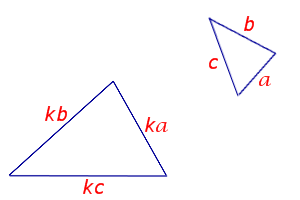
Формулировка признака подобия: Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны
|
Признаки подобия прямоугольных треугольников
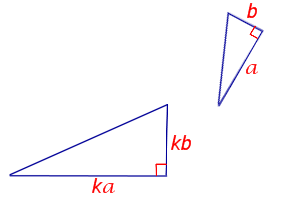
| Признак подобия прямоугольных треугольников по двум катетам |
|
Формулировка признака подобия прямоугольных треугольников: Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.
|
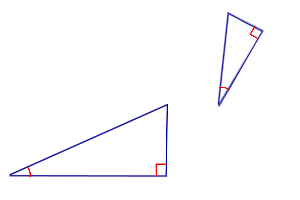
| Признак подобия прямоугольных треугольников по острому углу |
|
Формулировка признака подобия прямоугольных треугольников: Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.
|
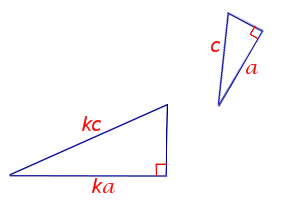
| Признак подобия прямоугольных треугольников по гипотенузе и катету |
|
Формулировка признака подобия прямоугольных треугольников: Если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и катету другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.
|
СЛЕДСТВИЕ 1. Прямая, пересекающая треугольник и параллельная стороне треугольника, отсекает от этого треугольника подобный треугольник (рис. 3).
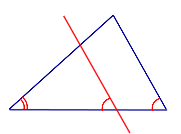
Рис.3
СЛЕДСТВИЕ 2. Отношение площадей подобных треугольников равно квадрату коэффициента подобия (рис. 4)
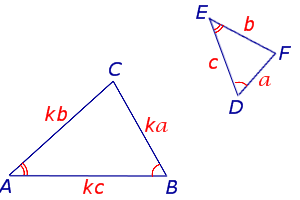
Рис.4