Справочник по математике Геометрия (Планиметрия)
Геометрия (Планиметрия) Треугольники
Треугольники
Свойства и признаки прямоугольного треугольника
| Определение прямоугольного треугольника |
|
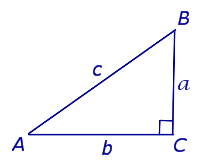
Определение Треугольник, у которого один из углов равен 90°, называют прямоугольным треугольником. Сторону, лежащую против угла в 90°, называют гипотенузой, две другие стороны называют катетами. |
| Свойство катетов прямоугольного треугольника |
|
Свойство Длины катетов прямоугольного треугольника меньше длины гипотенузы. |
| Определение равнобедренного прямоугольного треугольника |
|
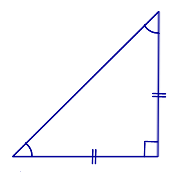
Определение Равнобедренным прямоугольным треугольником называют такой прямоугольный треугольник, у которого равны катеты. |
| Свойство углов равнобедренного прямоугольного треугольника |
|
Свойство Острые углы равнобедренного прямоугольного треугольника равны 45°. |
| Свойство прямоугольного треугольника с углом в 30° |
|
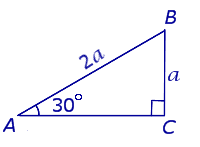
Свойство Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы. |
| Признак прямоугольного треугольника с углом в 30° |
|
Признак Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30°. |
| Свойство медианы, проведённой к гипотенузе прямоугольного треугольника |
|
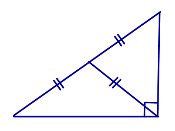
Свойство Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы. |
| Признак прямоугольного треугольника |
|
Признак Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным. |
| Свойство окружности, описанной около прямоугольного треугольника |
|
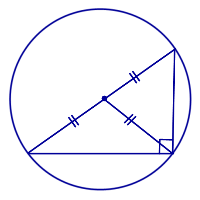
Свойство Середина гипотенузы прямоугольного треугольника является центром описанной около него окружности. |
| Признак прямоугольного треугольника |
|
Признак Если в треугольнике центр описанной окружности лежит на одной из сторон, то этот треугольник является прямоугольным треугольником, а центр описанной окружности совпадает с серединой гипотенузы. |
| Теорема Пифагора (свойство прямоугольного треугольника) |
|
Теорема Пифагора В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов c2 = a2 + b2 |
| Обратная теорема Пифагора (признак прямоугольного треугольника) |
|
Обратная теорема Пифагора Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным |