Занятия будут проходить 1 раз в неделю по 90 минут

Подробности по телефону   (495) 509-28-10

Нам не все равно, как Вы сдадите экзамены!

А Вам?

Справочник по математике

Геометрия (Планиметрия)

Углы

Углы на плоскости

      Углом называют часть плоскости, ограниченную двумя лучами, выходящими из одной точки. Лучи,ограничивающие угол, называют сторонами угла. Точку, из которой выходят лучи, называют вершиной угла.

      Схему обозначения углов рассмотрим на примере угла, изображенного на рисунке 1.

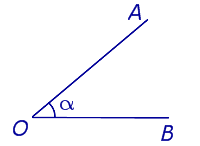
Рис.1

      Изображенный на рисунке 1 угол можно обозначить тремя способами: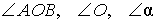

      Углы называют равными углами, если их можно совместить.

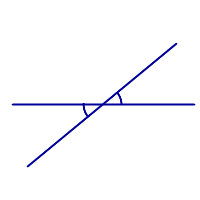
      Если при пересечении двух прямых образуются четыре равных угла, то такие углы называют прямыми углами (рис.2). Пересекающиеся прямые линии, образующие прямые углы, называют перпендикулярными прямыми.

Рис.2

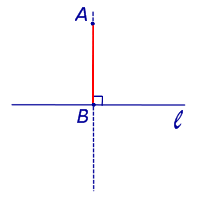
      Если через точку A, не лежащую на прямой l, проведена прямая, перпендикулярная к прямой l и пересекающая прямую l точке B, то говорят, что из точки B опущен перпендикупяр AB на прямую l (рис.3). Точку B называют основанием перпендикуляра AB.

Рис.3

      Замечание. Длину отрезка AB называют расстоянием от точки A до прямой l.

      Углом в 1° (один градус) называют угол, составляющий одну девяностую часть прямого угла.

      Угол, в k раз больший угла в 1°, называют углом в k° ( k градусов).

      Углы измеряют также и в радианах. О радианах можно прочитать в разделе нашего справочника «Измерение углов. Градусы и радианы».

Таблица 1 – Типы углов в зависимости от величины в градусах

Рисунок	Типы углов	Свойства углов
	Прямой угол	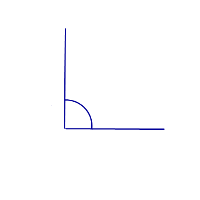Прямой угол равен 90°
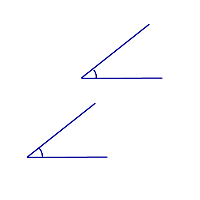
	Острый угол	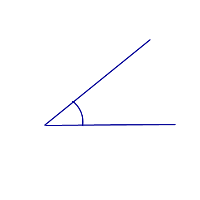Острый угол меньше 90°
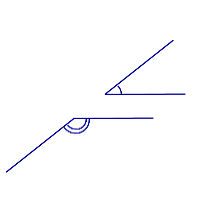
	Тупой угол	Тупой угол больше 90°, но меньше 180°
	Развернутый угол	Развернутый угол равен 180°
	Угол больший, чем развернутый	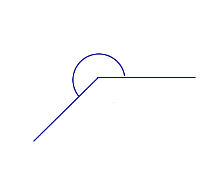Такой угол больше 180°, но меньше 360°
	Полный угол	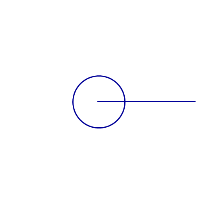Полный угол равен 360°
	Угол, равный нулю	Такой угол равен 0°

Прямой угол

Свойство: Прямой угол равен 90°

Острый угол

Свойство: Острый угол меньше 90°

Тупой угол

Свойство: Тупой угол больше 90°, но меньше 180°

Развернутый угол

Свойство: Развернутый угол равен 180°

Угол больший, чем развернутый

Свойство: Такой угол больше 180°, но меньше 360°

Полный угол

Свойство: Полный угол равен 360°

Угол, равный нулю

Свойство: Такой угол равен 0°

Таблица 2 – Типы углов в зависимости расположения сторон

Рисунок	Типы углов	Свойства углов
	Вертикальные углы	Вертикальные углы равны
	Смежные углы	Сумма смежных углов равна 180°
	Углы с соответственно параллельными сторонами	Углы с соответственно параллельными сторонами равны, если оба являются острыми или оба являются тупыми
		Сумма  углов с соответственно параллельными сторонами равна 180°, если один из них острый, а другой тупой
	Углы с соответственно перпендикулярными сторонами	Углы с соответственно перпендикулярными сторонами равны, если оба являются острыми или оба являются тупыми
		Сумма углов с соответственно перпендикулярными сторонами равна 180°, если один из них острый, а другой тупой

Вертикальные углы

Свойство вертикальных углов: Вертикальные углы равны

Смежные углы

Свойство смежных углов: Сумма смежных углов равна 180°

Углы с соответственно параллельными сторонами

Свойство углов с соответственно параллельными сторонами: Углы с соответственно параллельными сторонами равны, если оба являются острыми или оба являются тупыми

Свойство углов с соответственно параллельными сторонами: Сумма  углов с соответственно параллельными сторонами равна 180°, если один из них острый, а другой тупой

Углы с соответственно перпендикулярными сторонами

Свойство углов с соответственно перпендикулярными сторонами: Углы с соответственно перпендикулярными сторонами равны, если оба являются острыми или оба являются тупыми

Свойство углов с соответственно перпендикулярными сторонами: Сумма углов с соответственно перпендикулярными сторонами равна 180°, если один из них острый, а другой тупой

      Определение. Биссектрисой угла называют луч, делящий угол пополам.

      Задача. Доказать, что биссектрисы смежных углов перпендикулярны.

      Решение. Рассмотрим рисунок 4.

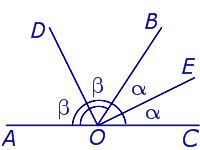
Рис.4

      На этом рисунке углы AOB и BOC – смежные, а лучи OE и OD – биссектрисы этих углов. Поскольку

2α + 2β = 180°.

то

α + β = 90°,

что и требовалось доказать.

   На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

      Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

подготовительные курсы для школьников 8, 9, 10 и 11 классов

      У нас также для школьников организованы

индивидуальные занятия с репетиторами по математике и русскому языку

МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»