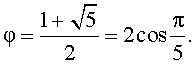Справочник по математикеАрифметика Золотое отношение

Золотое отношение (золотое сечение)

Содержание

	Золотое отношение (золотое сечение)
	Правильный пятиугольник и его связь с золотым отношением

Золотое отношение (золотое сечение)

Рассмотрим отрезок   AB   и точку   C ,   расположенную внутри него.

Говорят, что точка   C   делит отрезок   AB   в золотом отношении (золотом сечении), если длина отрезка   AB   так относится к длине отрезка   AC ,   как длина отрезка   AC   относится к длине отрезка   CB .   При этом самим золотым отношением (золотым сечением) называют отношение длины отрезка   AB   к длине отрезка   AC .

Термин «золотое отношение» имеет ряд синонимов: золотое сечение, золотая пропорция, гармоническая пропорция, золотое число, деление отрезка в крайнем и среднем отношении.

Следуя исторической традиции, будем золотое отношение обозначать символом   φ .   Для того, чтобы найти значение   φ ,   введем для длин отрезков   AB   и   AC   обозначения:

|AB| = x,       |AC| = y .

Тогда длина отрезка   CB   будет выражена формулой:

|CB| = x – y ,

причем числа   x   и   y   будут удовлетворять неравенствам:

x > 0,   y > 0,   x – y > 0.

В случае, когда точка   C   делит отрезок   AB   в золотом отношении, числа   x   и   y   удовлетворяют уравнению:

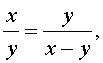
где

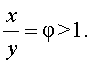
Выведем уравнение для переменной   φ :

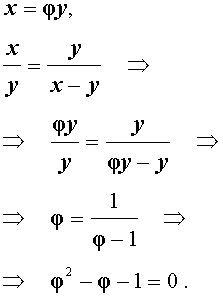
Следовательно,

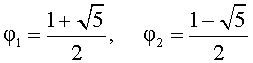
Поскольку   φ > 1 , то второй корень должен быть отброшен.

Итак, золотое отношение

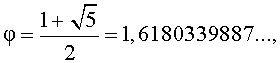
что и требовалось получить.

Правильный пятиугольник и его связь с золотым отношением

Золотое отношение (золотое сечение) встречается в различных областях человеческой деятельности: в скульптуре, архитектуре, живописи, музыке и т.д.

Приведем пример использования золотого отношения в планиметрии. Для этого рассмотрим правильный пятиугольник   A₁A₂A₃A₄A₅ ,   вписанный в окружность радиуса   R   с центром   O .

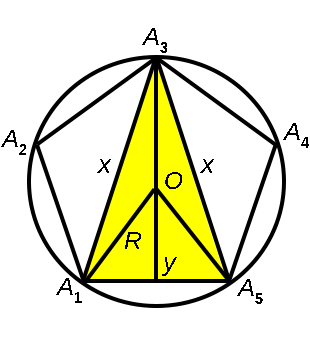
Заметив, что длины всех диагоналей пятиугольника равны, обозначим длину стороны пятиугольника символом   y ,   а длину диагоналей символом   x .

Теперь рассмотрим треугольник   A₁A₃A₅ .   Этот треугольник является равнобедренным треугольником с основанием   A₁A₅   и боковыми сторонами   A₁A₃   и   A₃A₅ ,   причем

  A₁A₅ = y,       A₁A₃ = A₃A₅ = x .

Кроме того,

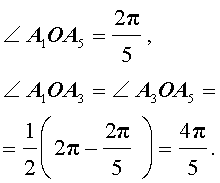
Следовательно,

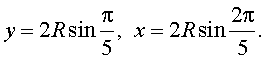
Теперь, воспользовавшись тем, что

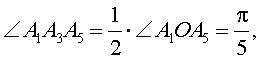
применим для треугольника   A₁A₃A₅   теорему косинусов:

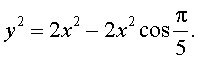
Разделив это равенство на   y²,   и заметив, что

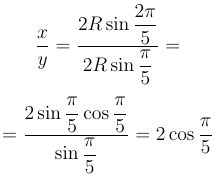
получим соотношение:

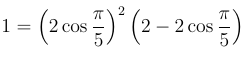
Если в этом соотношении ввести, для упрощения записи, переменную   d   по формуле

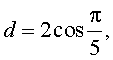
то возникает уравнение:

d ³ – 2d ² + 1 = 0.

Для того, чтобы решить это уравнение, разложим его левую часть на множители:

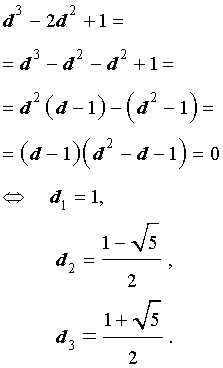
В силу того, что

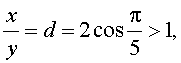
то первый и второй корни должны быть отброшены. Следовательно,

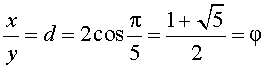
т.е. является золотым отношением.

В результате мы получили, что, во-первых, отношение диагонали правильного пятиугольника к стороне правильного пятиугольника равно золотому отношению, а, во-вторых, что для самого золотого отношения справедлива формула: