Справочник по математике
Арифметика Обыкновенные и десятичные дроби
Дробь. Правильные и неправильные дроби. Смешанные числа
Содержание
 |
Дробь. Числитель и знаменатель дроби |
|
Правильные и неправильные дроби. Смешанные числа |
|
Основное свойство дроби, сокращение дробей, несократимая дробь |
Дробь. Числитель и знаменатель дроби
ОПРЕДЕЛЕНИЕ 1. Дробью называют одну или несколько одинаковых долей (частей) предмета или некоторой величины.
Дробь записывают при помощи двух натуральных чисел, одно из которых стоит над горизонтальной чертой, а второе – под нею.
ОПРЕДЕЛЕНИЕ 2. Число, стоящее над чертой, называют числителем дроби. Число, стоящее под чертой, называют знаменателем дроби.Числитель и знаменатель называют членами дроби.
Знаменатель дроби показывает, на сколько одинаковых долей мы делим предмет или величину, а числитель дроби показывает, сколько таких долей взято.
Например, дробь
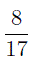
у которой числитель равен 8 , а знаменатель равен 17 , означает, что предмет или величину мы делим на 17 равных долей (частей) и берем 8 таких долей.
ПРИМЕР 1. В классе 25 учеников, из которых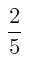 
посещают театральный кружок. Сколько учеников ходят в театральный кружок?
РЕШЕНИЕ. Для решения примера нужно 25 учеников разделить на 5 частей и взять 2 таких части.
ОТВЕТ. 10 учеников.
ПРИМЕР 2. Турист в первый день похода прошел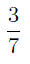 
намеченного маршрута, а во второй день – оставшиеся 24 километра. Сколько всего километров прошел турист?
РЕШЕНИЕ. Весь маршрут разделен на 7 равных частей, 3 из которых турист прошел в первый день (рис. 1).
| 1 день |
| 1 день |
| 1 день |
| 2 день |
| 2 день |
| 2 день |
| 2 день |
Рис. 1
Из рисунка 1 видно, что 24 километра составляют 4 из 7 частей маршрута. Таким образом, 1 часть маршрута равна
24 : 4 = 6 (км) ,
а весь маршрут равен
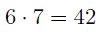(км) .
ОТВЕТ. 42 километра.
ЗАМЕЧАНИЕ. Если не указано, от какого предмета или какой величины берется дробь, то считают, что дробь взята от числа 1 .
Термин дробь имеет синонимы: простая дробь, обыкновенная дробь, рациональная дробь, дробное число.
Правильные и неправильные дроби. Смешанные числа
ОПРЕДЕЛЕНИЕ 3. Если у дроби числитель меньше знаменателя, то ее называют правильной дробью. В противном случае – неправильной дробью.
Из этого определения, в частности, вытекает, что правильная дробь меньше единицы, а неправильная - больше единицы или равна единице.
ПРИМЕР 3
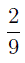– правильная дробь, 
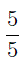и 
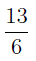– неправильные дроби.
Неправильную дробь всегда можно представить в виде суммы целого числа и правильной дроби. Эту операцию называют выделением целой части из неправильной дроби и осуществляют при помощи деления с остатком числителя неправильной дроби на знаменатель.
ПРИМЕР 4 .
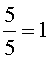
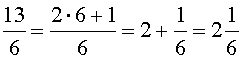
Число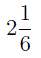 
является примером смешанного числа. Целое число 2 и правильную дробь 
называют целой и дробной частью смешанного числа соответственно.
Любое смешанное число всегда можно обратить в неправильную дробь, например,
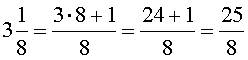
Основное свойство дроби, сокращение дробей, несократимая дробь
Основным свойством дроби называют следующее
УТВЕРЖДЕНИЕ. Дробь превращается в равную дробь, если её числитель и знаменатель умножить или разделить на одно и то же число.
ОПРЕДЕЛЕНИЕ 4. Операцию, при которой числитель и знаменатель дроби делят на одно и то же число, называют сокращением дроби.
ПРИМЕР 5.
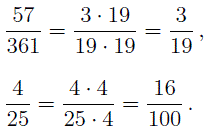
ОПРЕДЕЛЕНИЕ 5. Если числитель и знаменатель дроби не имеют общих делителей, то такую дробь называют несократимой.
При помощи сокращений любую дробь можно превратить в равную ей несократимую дробь.