Справочник по математике Арифметика
Арифметика Делимость и деление с остатком
Делимость и деление с остатком
Наименьшее общее кратное
Содержание
 |
Общее кратное. Наименьшее общее кратное |
 |
Алгоритм нахождения наименьшего общего кратного |
 |
Связь между наибольшим общим делителем и наименьшим общим кратным двух натуральных чисел |

Общее кратное. Наименьшее общее кратное
ОПРЕДЕЛЕНИЕ 1. Если натуральное число a делится на натуральное число b , то число a называют кратным числу b .
ОПРЕДЕЛЕНИЕ 2. Общим кратным нескольких натуральных чисел называют натуральное число, которое является кратным для каждого из этих чисел.
В частности, общим кратным нескольких чисел является произведение этих чисел.
ОПРЕДЕЛЕНИЕ 3. Наименьшее из общих кратных нескольких натуральных чисел называют наименьшим общим кратным (НОК) этих чисел.
Алгоритм нахождения наименьшего общего кратного
Рассмотрим алгоритм нахождения наименьшего общего кратного нескольких чисел на следующем примере.
ПРИМЕР. Найти наименьшее общее кратное чисел 100 , 750 и 800 .
РЕШЕНИЕ. Разложим эти числа на простые множители:
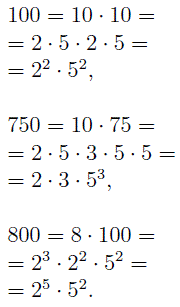
Простой множитель 2 в первое разложение на множители входит в степени 2 , во второе разложение – в степени 1 , в третье разложение – в степени 5 . Обозначим наибольшую из этих степеней буквой k . Очевидно, что k = 5 .
Простой множитель 3 в первое разложение на множители входит в степени 0 (другими словами, множитель 3 в первое разложение на множители вообще не входит), во второе разложение входит в степени 1 , в третье разложение – в степени 0 . Обозначим наибольшую из этих степеней буквой l . Очевидно, что l = 1 .
Простой множитель 5 в первое разложение на множители входит в степени 2 , во второе разложение – в степени 3 , в третье разложение – в степени 2 . Обозначим наибольшую из этих степеней буквой m . Очевидно, что m = 3 .
Теперь рассмотрим число:
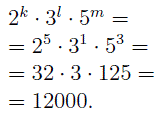
то число и есть наименьшее общее кратное чисел 100 , 750 и 800 .
ОТВЕТ: 12000 .
Связь между наибольшим общим делителем и наименьшим общим кратным двух натуральных чисел
УТВЕРЖДЕНИЕ. Наименьшее общее кратное двух чисел можно найти, разделив произведение этих чисел на их наибольший общий делитель.
Действительно, рассмотрим, например, два числа: 10 и 75 . Разлагая эти числа на простые множители, получим
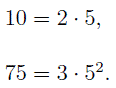
Используя алгоритмы нахождения наибольшего общего делителя и наименьшего общего кратного чисел, получаем, что наибольший общий делитель этих чисел равен 5 , а наименьшее общее кратное этих чисел равно 150 . Поскольку произведение чисел 10 и 75 равно 750 , то справедливо соотношение
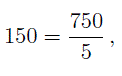
что и требовалось показать.
ЗАМЕЧАНИЕ. Поскольку наибольший общий делитель двух взаимно простых чисел равен 1 , то наименьшее общее кратное двух взаимно простых чисел равно их произведению.
