Справочник по математике Арифметика
Арифметика Делимость и деление с остатком
Делимость и деление с остатком
Наибольший общий делитель. Взаимно простые числа
Содержание
 |
Общий делитель нескольких натуральных чисел. Наибольший общий делитель. Взаимно простые числа |
 |
Алгоритм нахождения наибольшего общего делителя |

Общий делитель нескольких натуральных чисел. Наибольший общий делитель. Взаимно простые числа
ОПРЕДЕЛЕНИЕ 1. Общим делителем нескольких натуральных чисел называют число, которое является делителем каждого из этих чисел.
ОПРЕДЕЛЕНИЕ 2. Самый большой из общих делителей называют наибольшим общим делителем (НОД).
ПРИМЕР 1. Общими делителями чисел 30 , 45 и 60 будут числа 1 , 3 , 5 , 15 . Наибольшим общим делителем этих чисел будет
НОД ( 30 , 45 , 10) = 15 .
ОПРЕДЕЛЕНИЕ 3. Если наибольший общий делитель нескольких чисел равен 1 , то эти числа называют взаимно простыми.
ПРИМЕР 2. Числа 40 и 3 будут взаимно простыми числами, а числа 56 и 21 не являются взаимно простыми, поскольку у чисел 56 и 21 есть общий делитель 7 , который больше, чем 1.
ЗАМЕЧАНИЕ. Если числитель дроби и знаменатель дроби являются взаимно простыми числами, то такая дробь несократима.
Алгоритм нахождения наибольшего общего делителя
Рассмотрим алгоритм нахождения наибольшего общего делителя нескольких чисел на следующем примере.
ПРИМЕР 3. Найти наибольший общий делитель чисел 100, 750 и 800 .
РЕШЕНИЕ. Разложим эти числа на простые множители:
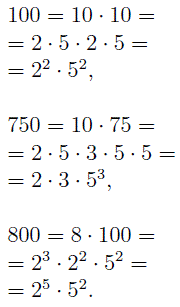
Простой множитель 2 в первое разложение на множители входит в степени 2 , во второе разложение – в степени 1 , в третье разложение – в степени 5 . Обозначим наименьшую из этих степеней буквой a . Очевидно, что a = 1 .
Простой множитель 3 в первое разложение на множители входит в степени 0 (другими словами, множитель 3 в первое разложение на множители вообще не входит), во второе разложение входит в степени 1 , в третье разложение – в степени 0 . Обозначим наименьшую из этих степеней буквой b . Очевидно, что b = 0 .
Простой множитель 5 в первое разложение на множители входит в степени 2 , во второе разложение – в степени 3 , в третье разложение – в степени 2 . Обозначим наименьшую из этих степеней буквой c . Очевидно, что c = 2 .
Теперь рассмотрим число:
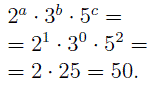
Это число и есть наибольший общий делитель чисел 100, 750 и 800 .
ОТВЕТ: 50 .
ЗАМЕЧАНИЕ. Чтобы сократить дробь, нужно её числитель и знаменатель разделить на их наибольший общий делитель.
