Справочник по математикеГеометрия (Стереометрия) Проекции геометрических фигур

Длина ортогональной проекции отрезка. Площадь ортогональной проекции многоугольника

Содержание

	Длина проекции отрезка.
	Площадь проекции треугольника.
	Площадь проекции многоугольника.

Длина ортогональной проекции отрезка

Рассмотрим сначала двугранный угол   φ ,   образованный полуплоскостями   α   и   β ,   пересекающимися по прямой   AB ,   и отрезок   CD ,   лежащий в полуплоскости   β   и перпендикулярный прямой   AB   (рис. 1).

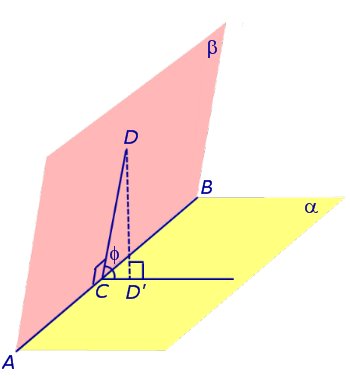
Рис.1

На этом рисунке символом   D'   обозначена ортогональная проекция точки   D   на плоскость   α .   Отрезок   CD'   является проекцией отрезка   CD   на плоскость   α .

Из треугольника   CDD'   можно найти длину стороны   CD',   если известна длина отрезка   CD   и угол   φ:

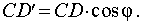(1)

Теперь рассмотрим тот же двугранный угол, но отрезок   CD   расположим на полуплоскости   β   так, что прямая   CD   параллельна ребру   двугранного угла   AB   (рис. 2).

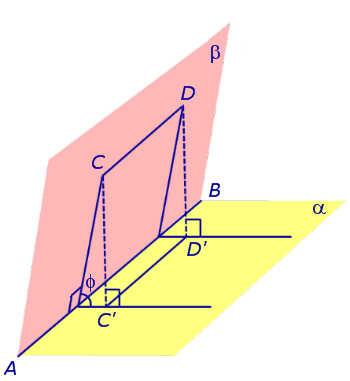
Рис.2

На рисунке 2 символами   C'   и   D'   обозначены проекции точек   C   и   D   на плоскость   α .

Отрезок   C'D'   является проекцией отрезка   CD   на плоскость   α .   Поскольку   CDD'C'   – прямоугольник, то длина стороны   CD   равна длине стороны   C'D' ,   то есть

Теперь рассмотрим наиболее сложный случай, когда отрезок   CD   длины   a   расположен на полуплоскости   β   так, что вершина   C   лежит на прямой   AB,   а угол 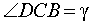(рис. 3).

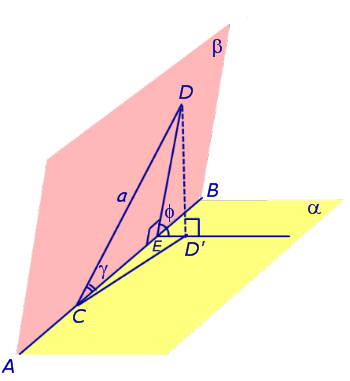
Рис.3

Обозначим буквой   E   основание перпендикуляра, опущенного в плоскости   β   из точки   D   на прямую   AB .   Обозначим через   D'   проекцию точки   D   на плоскость   α .   Тогда из прямоугольных треугольников   CDE   и   DED'   получаем следующие равенства:

DE = a sin γ,     CE = a cos γ,     ED' = DE cos φ = a sin γ cos φ ,

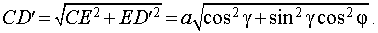
Итак, длина проекции отрезка   CD   равна

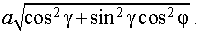(3)

ЗАМЕЧАНИЕ 1. Мы оставляем читателю в качестве полезного упражнения возможность найти длину проекции отрезка   CD   в случае, когда его концы не лежат на ребре   AB   двугранного угла.

ЗАМЕЧАНИЕ 2. При   γ = 90°   отрезок   CD   перпендикулярен ребру   AB   двугранного угла, и формула (3) приобретает вид (1). При   γ = 0°   отрезок   CD   параллелен ребру   AB   двугранного угла, и формула (3) приобретает вид (2).

Площадь проекции треугольника

Рассмотрим треугольник   CDE,   расположенный в полуплоскости   β   так, что сторона   CE   лежит на ребре   AB   двугранного угла (рис. 4).

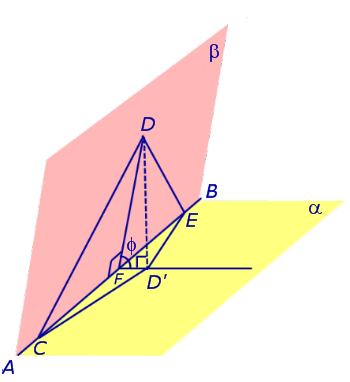
Рис.4

Буквой   F   обозначено основание перпендикуляра, опущенного из точки   D   на прямую   AB .   Символом   D'   обозначена проекция точки   D   на плоскость   α .

Треугольник   CD'E   является проекцией треугольника   CDE   на плоскость   α .   Площадь треугольника   CDE   находится по формуле:

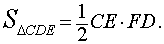
Площадь треугольника   CD'E   находится по формуле:

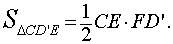
В силу формулы (1)

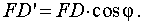
Следовательно,

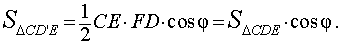(4)

Теперь рассмотрим треугольник   CDE,   расположенный в полуплоскости   β   так, что на ребре   AB   двугранного угла лежит только вершина   C   (рис. 5).

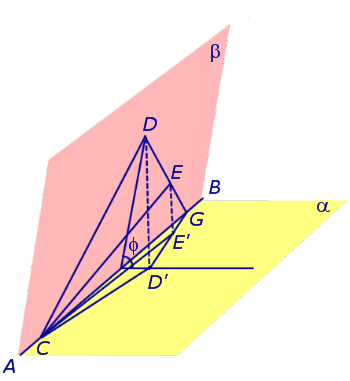
Рис.5

Буквой   G   обозначим точку пересечения прямой   DE   с прямой   AB.   Точки   D'   и   E'   – проекции точек   D   и   E   на плоскость   α.   Треугольник   CD'E'   является проекцией треугольника   CDE ,   а треугольник   CE'G   – проекцией треугольника   CEG .   Воспользовавшись формулой (4), получаем

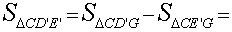
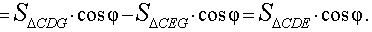
Таким образом, справедлива формула

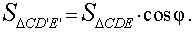(5)

ЗАМЕЧАНИЕ 3. Формулу (5) мы получили в предположении о том, что точка   C   лежит на ребре   AB   двугранного угла. Небольшое дополнение к приведенному доказательству позволяет отказаться от этого ограничения. Мы оставляем доказательство этого факта читателю в качестве полезного и несложного упражнения.

Площадь проекции многоугольника

Рассмотрим произвольный выпуклый n – угольник, расположенный в полуплоскости   β,   и проведем все диагонали многоугольника из вершины   A₁   (рис. 6).

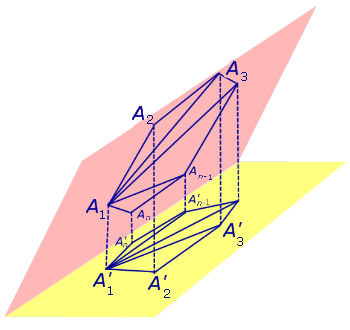
Рис.6

В результате многоугольник разбивается на треугольники   A₁A₂A₃, A₁A₃A₄, ... , A₁A_n-1A_n.   Если обозначить через   A'₁, A'₂, ... , A'_n   проекции точек   A₁, A₂, ... , A_n   на плоскость   α ,   то, применяя к каждому из треугольников   A₁A₂A₃, A₁A₃A₄, ... , A₁A_n-1A_n   формулу (5), получаем формулу для площади проекции многоугольника

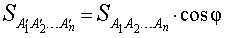(6)

Таким образом, площадь проекции многоугольника, лежащего в плоскости   β,   на плоскость   α   равна площади этого многоугольника, умноженной на косинус угла между плоскостями.