Справочник по математике Геометрия (Стереометрия)
Геометрия (Стереометрия) Цилиндры
Цилиндры
Цилиндры
Содержание
 |
Основные определения и свойства цилиндра |
 |
Сечения цилиндра |
 |
Объем цилиндра. Площадь боковой поверхности цилиндра. Площадь полной поверхности цилиндра |

Основные определения и свойства цилиндра
ОПРЕДЕЛЕНИЯ
 |
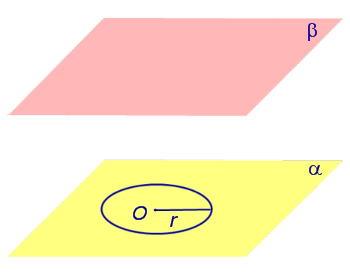
Рассмотрим две параллельные плоскости α и β и произвольную окружность радиуса r с центром в точке O, лежащую в плоскости α (рис. 1).
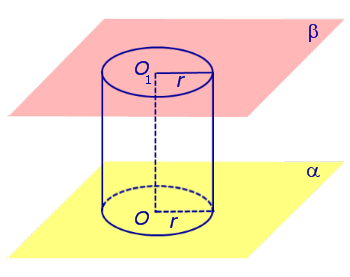
Рис.1 Если из каждой точки окружности опустить перпендикуляр на плоскость β, то основания этих перпендикуляров образуют на плоскости β окружность радиуса r, центр O1 которой является основанием перпендикуляра, опущенного из точки O на плоскость β (рис.2).
Рис.2 Отрезок перпендикуляра, опущенного из любой точки окружности с центром O на плоскость β , который заключен между плоскостями α и β , называют образующей цилиндра. |
 |
Совокупность всех образующих цилиндра называют цилиндрической поверхностью. |
 |
Фигуру, ограниченную цилиндрической поверхностью и плоскостями α и β, называют цилиндром. |
 |
Отрезок OO1 называют осью цилиндра . |
 |
Радиус окружности на плоскости α с центром в точке O называют радиусом цилиндра. |
 |
Расстояние между плоскостями α и β , называют высотой цилиндра. |
 |
Круги с центрами O и O1 на плоскостях α и β , называют основаниями цилиндра. |
 |
Цилиндрическую поверхность часто называют боковой поверхностью цилиндра. Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра. |
ЗАМЕЧАНИЕ 1. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.
ЗАМЕЧАНИЕ 2. Прямая OO1 является осью симметрии цилиндра, а середина отрезка OO1 является центром симметрии цилиндра.
Сечения цилиндра
ОПРЕДЕЛЕНИЕ 2. Сечением цилиндра называют пересечение цилиндра с плоскостью.
Если сечение проходит через ось цилиндра, то такое сечение называют осевым сечением цилиндра (рис. 3).
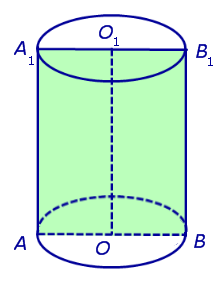
Рис.3
На рисунке 3 изображено одно из осевых сечений цилиндра – прямоугольник AA1B1B .
ЗАМЕЧАНИЕ 3. Каждое осевое сечение цилиндра с радиусом r и высотой h является прямоугольником со сторонами 2r и h .
ОПРЕДЕЛЕНИЕ 3. Перпендикулярным сечением цилиндра называют сечение, перпендикулярное оси цилиндра (рис. 4).
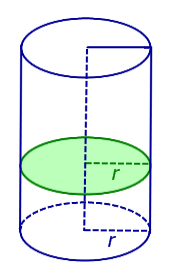
Рис.4
ЗАМЕЧАНИЕ 4. Любым перпендикулярным сечением цилиндра будет круг радиуса r .
ЗАМЕЧАНИЕ 5. Более подробно случаи взаимного расположения цилиндра и плоскости рассматриваются в разделе нашего справочника «Взаимное расположение цилиндра и плоскости в пространстве».
Объем цилиндра. Площадь боковой поверхности цилиндра.
Площадь полной поверхности цилиндра
Для цилиндра с радиусом r и высотой h (рис. 5)
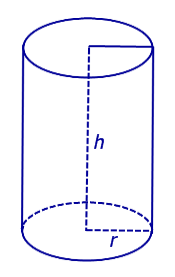
Рис.5
введем следующие обозначения
| V | объем цилиндра |
| Sбок | площадь боковой поверхности цилиндра |
| Sполн | площадь полной поверхности цилиндра |
| Sосн | площадь основания цилиндра |
Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности цилиндра:
Sосн = πr2,
V = Sосн h = πr2h,
Sбок= 2πrh,
Sполн = 2πr2 + 2πrh = 2π(r + h).
ЗАМЕЧАНИЕ 6. Формула объема цилиндра V = πr2h может быть получена из формулы объема правильной n – угольной призмы
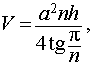
при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.