Справочник по математике Геометрия (Стереометрия)
Геометрия (Стереометрия) Прямые и плоскости в пространстве
Прямые и плоскости в пространстве
Двугранные углы. Углы между плоскостями. Перпендикулярность плоскостей
ОПРЕДЕЛЕНИЯ
 |
Двугранным углом называют часть пространства, ограниченную двумя полуплоскостями с общей границей (рис. 1)
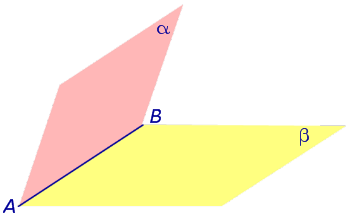
Рис.1
|
 |
Полуплоскости α и β , ограничивающие двугранный угол, называют гранями двугранного угла, а их общую границу AB называют ребром двугранного угла.
|
 |
Двугранные углы называют равными двугранными углами, если их можно совместить.
|
 |
При пересечении двух плоскостей образуются четыре двугранных угла (рис. 2). Наименьший из этих углов обычно и называют углом между плоскостями.

Рис.2
|
 |
Если при пересечении двух плоскостей образовалось 4 равных двугранных угла, то такие двугранные углы называют прямыми двугранными углами, а сами плоскости называют перпендикулярными плоскостями (рис. 3).
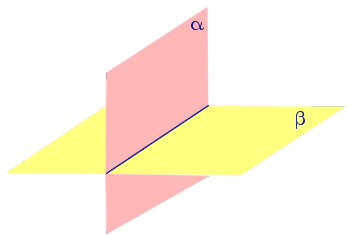
Рис.3
|
 |
Выберем произвольную точку С на ребре AB двугранного угла и проведем через нее перпендикуляры CD и CE в каждой из граней двугранного угла. Угол DCE, образованный перпендикулярами CD и CE, называют линейным углом двугранного угла (рис. 4).
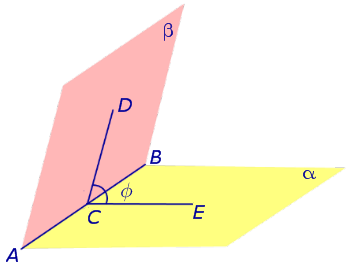
Рис.4
|
На рисунке 4 угол φ является линейным углом двугранного угла с гранями α и β и ребром AB .
Линейные углы двугранных углов используются, в частности, для того, чтобы измерять двугранные углы. Например, если линейный угол двугранного угла равен 30° (или 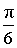 радиан), то и двугранный угол равен 30° (
радиан), то и двугранный угол равен 30° (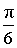 радиан). Соответственно, прямой двугранный угол равен 90° (
радиан). Соответственно, прямой двугранный угол равен 90° ( радиан).
радиан).
 Геометрия (Стереометрия)
Геометрия (Стереометрия) Прямые и плоскости в пространстве
Прямые и плоскости в пространстве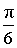 радиан), то и двугранный угол равен 30° (
радиан), то и двугранный угол равен 30° (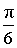 радиан). Соответственно, прямой двугранный угол равен 90° (
радиан). Соответственно, прямой двугранный угол равен 90° ( радиан).
радиан).




