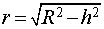Справочник по математике
Геометрия (Стереометрия) Сферы и шары
Взаимное расположение сферы и плоскости в пространстве
Рассмотрим сферу радиуса R с центром в точке O и плоскость α . Обозначим символом O1 основание перпендикуляра, опущенного из точки O на плоскость α , и обозначим буквой h расстояние от точки O до плоскости α (т. е. длину отрезка OO1).
В зависимости от соотношения между R и h можно составить следующую таблицу, в которой описаны все возможные случаи взаимного расположения сферы и плоскости в пространстве.
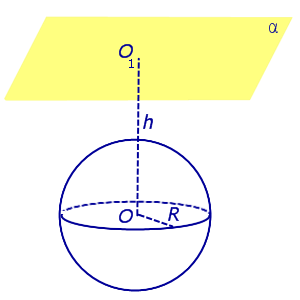
| Сфера и плоскость не имеют общих точек (не пересекаются) |
|
Свойства: Сфера и плоскость не пересекаются тогда и только тогда, когда h > R |
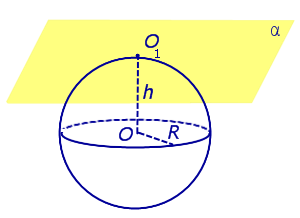
| Сфера и плоскость имеют единственную общую точку (касаются) |
|
Определение Если сфера и плоскость имеют единственную общую точку, то плоскость называют касательной плоскостью к сфере, а их общую точку называют точкой касания. Свойства: Сфера и плоскость касаются тогда и только тогда, когда h = R Если сфера и плоскость α касаются, то радиус, проведенный в точку касания перпендикулярен плоскости α. Если сфера и плоскость α имеют общую точку и радиус, проведенный в эту точку, перпендикулярен плоскости α, то сфера и плоскость касаются. |
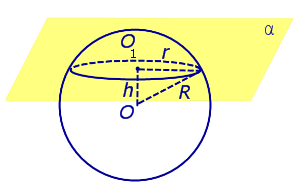
| Сфера и плоскость имеют более одной общей точки. Плоскость не проходит через центр сферы. |
|
Свойства: Пересечением сферы и плоскости является окружность радиуса r с центром в точке O1. В этом случае 0 < h < R ,
Отрезок OO1 перпендикулярен плоскости α. |
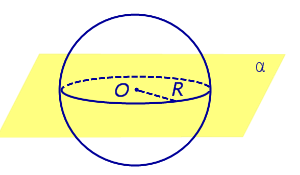
| Сфера и плоскость имеют более одной общей точки. Плоскость проходит через центр сферы. |
|
Свойства: Пересечением сферы и плоскости является окружность радиуса R с центром в точке O. В этом случае h = 0 . Если плоскость проходит через центр сферы, то часто говорят, что сфера и плоскость пересекаются по большому кругу. |
