Справочник по математикеГеометрия (Стереометрия) Прямые и плоскости в пространстве

Взаимное расположение двух прямых в пространстве. Признак скрещивающихся прямых. Угол между скрещивающимися прямыми

Содержание

	Взаимное расположение двух прямых в пространстве
	Признак скрещивающихся прямых
	Угол между скрещивающимися прямыми

Взаимное расположение двух прямых в пространстве

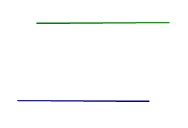
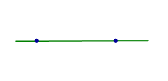
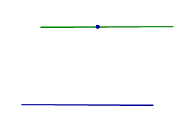
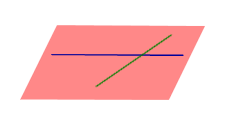
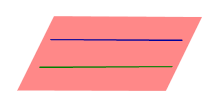
Все возможные случаи взаимного расположения двух прямых в пространстве представлены в таблице.

С перечисленными в предыдущей таблице случаями взаимного расположения двух прямых в пространстве близко связаны утверждения, представленные в таблице.

Признак скрещивающихся прямых

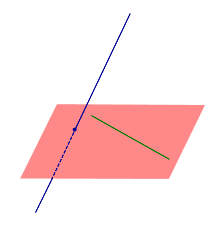
ПРИЗНАК СКРЕЩИВАЮЩИХСЯ ПРЯМЫХ. Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются (рис.1).

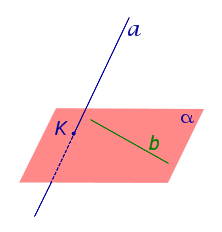
Рис.1

ДОКАЗАТЕЛЬСТВО.. Напомним, что две прямые называют скрещивающимися, если не существует плоскости, содержащей обе эти прямые, и будем доказывать признак скрещивающихся прямых методом «от противного»

Для этого предположим, что прямая   a,   пересекающая плоскость в точке K, и прямая b, лежащая в плоскости   α  (рис. 1), не являются скрещивающимися. Из этого предположения следует, что существует плоскость, содержащая обе эти прямые. Обозначим эту плоскость буквой  β  и докажем, что плоскость  β  совпадает с плоскостью  α. Действительно, поскольку обе плоскости   α  и   β проходят через прямую b и точку K, не лежащую на этой прямой, то они совпадают. Следовательно, прямая a лежит в плоскости. Мы получили противоречие с тем, что по условию прямая a пересекает плоскость, а не лежит в ней. Доказательство признака скрещивающихся прямых завершено.

Угол между скрещивающимися прямыми

ОПРЕДЕЛЕНИЕ. Углом между скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым (рис. 2).

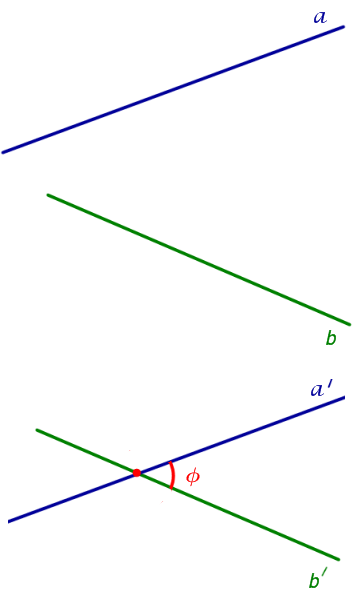
Рис.2

На рисунке 2 изображены скрещивающиеся прямые   a  и   b. Прямая a' параллельна прямой a, прямая b' параллельна прямой b. Прямые a' и b' пересекаются. Угол   φ  и является углом между скрещивающимися прямыми   a  и   b.

ЗАДАЧА. В кубе   ABCDA₁B₁C₁D₁   найти угол между прямыми   AB₁   и   BC₁.

РЕШЕНИЕ. Поскольку прямая   AB₁   пересекает плоскость   BB₁C₁   в точке   B₁,   которая не лежит на прямой   BC₁,   то по признаку скрещивающихся прямых прямые   AB₁   и   BC₁   скрещиваются (рис. 3).

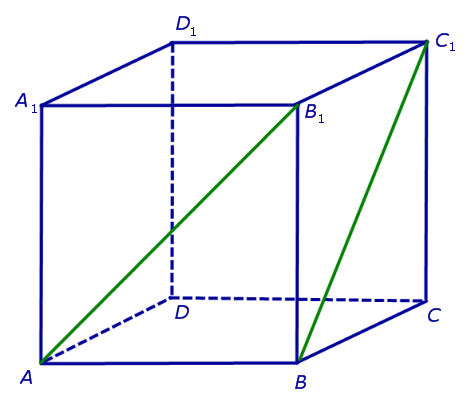
Рис.3

Для того, чтобы найти угол между прямыми   AB₁   и   BC₁, проведем в кубе диагональ боковой грани   AD₁   и диагональ верхнего основания   D₁B₁   (рис. 4).

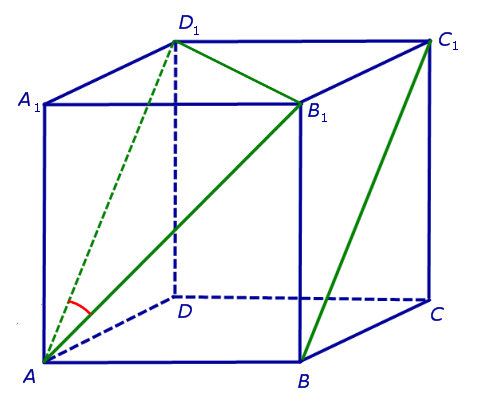
Рис.4

По определению угла между скрещивающимися прямыми угол   D₁AB₁   и является углом между прямыми AB₁   и   BC₁.   Поскольку треугольник   AD₁B₁   равносторонний, угол   D₁AB₁   равен   60°.

ОТВЕТ. 60°.

ЗАМЕЧАНИЕ. Для более глубокого усвоения понятия «Скрещивающиеся прямые» рекомендуем ознакомиться с разделами нашего сайта «Общий перпендикуляр к двум скрещивающимся прямым. Расстояние между скрещивающимися прямыми».