Справочник по математикеТригонометрия

Обратные тригонометрические функции

ОПРЕДЕЛЕНИЕ 1. Пусть число a удовлетворяет неравенству 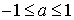. Число x называют арксинусом числа a и обозначают   x = arcsin a, если выполнены два условия:

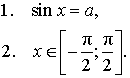
ОПРЕДЕЛЕНИЕ 2. Пусть число a удовлетворяет неравенству 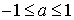. Число x называют арккосинусом числа a и обозначают   x = arccos a, если выполнены два условия:

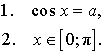
ОПРЕДЕЛЕНИЕ 3. Рассмотрим произвольное число a . Число x называют арктангенсом числа a и обозначают   x = arctg a, если выполнены два условия:

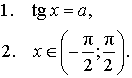
ОПРЕДЕЛЕНИЕ 4. Рассмотрим произвольное число a . Число x называют арккотангенсом числа a и обозначают   x = arcctg a, если выполнены два условия:

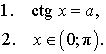
Арксинус, арккосинус, арктангенс и арккотангенс удовлетворяют, в частности, следующим соотношениям:

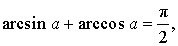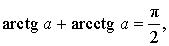arcsin (– a) = – arcsin a ,

arccos (– a) = π – arccos a ,

arctg (– a) = – arctg a ,

arcctg (– a) = π – arcctg a .

Обратными тригонометрическими функциями называют функции:

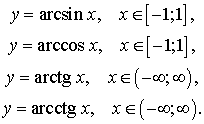
Графики этих функций изображены на рисунках 1, 2, 3, 4.

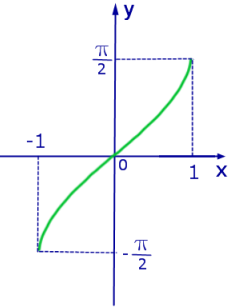
Рис. 1. График функции   y = arcsin x

ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ    y =arcsin x

x	y = arcsin x
– 1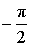
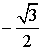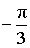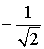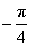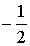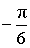0	0
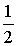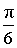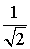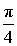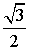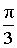1

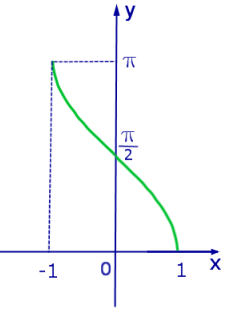
Рис. 2. График функции   y = arccos x

ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ   y = arccos x

x	y = arccos x
– 1	π
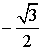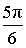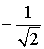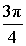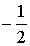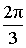0
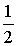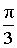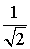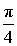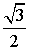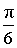1	0

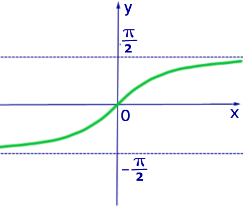
Рис. 3. График функции   y = arctg x

ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ   y = arctg x

x	y = arctg x
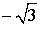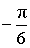– 1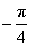
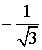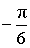0	0
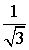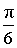1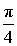

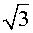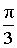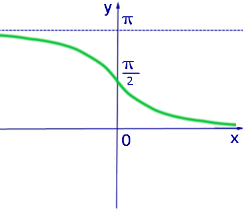
Рис. 4. График функции   y = arcctg x

ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ   y = arcctg x

x	y = arcctg x
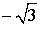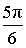– 1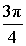
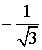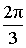0
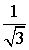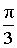1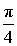

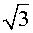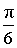ПРИМЕР. Решить уравнение

2 arcsin 2x = arccos 7x .

РЕШЕНИЕ. Возьмём косинус от обеих частей уравнения. Тогда в левой части уравнения получим:

cos ( 2 arcsin 2x ) = 1 – 2sin²( arcsin 2x ) =1 – 2 ( 2x )² = 1 – 8x² .

В правой части уравнения получим:

cos ( arccos 7x ) = 7x.

Следовательно, возникает квадратное уравнение:

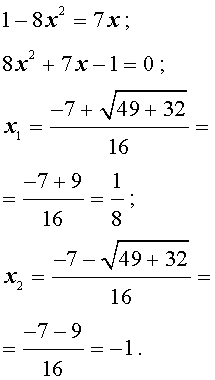
В силу того, что область определения обратных тригонометрических функций   y = arcsin x и   y = arccos x   имеет вид: 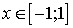, второй корень должен быть отброшен.

ОТВЕТ: