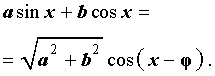Справочник по математике
Тригонометрия
Метод введения дополнительного угла (Метод введения вспомогательного аргумента)
Рассмотрим метод введения дополнительного угла на примере решения следующей задачи.
ЗАДАЧА. Найти наибольшее и наименьшее значения функции
| y = sin x + cos x. | (1) |
РЕШЕНИЕ. Заметив, что
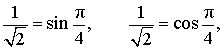
преобразуем правую часть формулы (1):
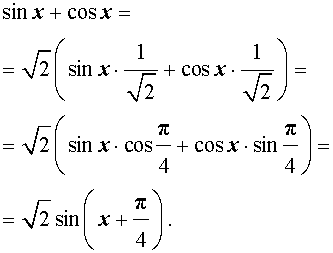
Отсюда вытекает, что выражение (1) можно переписать в виде:
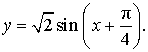
Поскольку
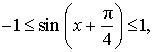
причем
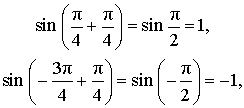
то
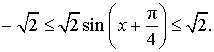
Следовательно,
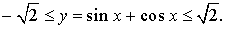
ОТВЕТ. Наибольшее значение функции (1) равно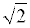 
, наименьшее значение функции (1) равно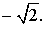 
ЗАМЕЧАНИЕ. В рассмотренной задаче угол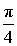 
и является дополнительным углом.
Теперь докажем формулу дополнительного угла (вспомогательного аргумента) в общем виде. Для этого рассмотрим выражение
| a sin x + bcos x | (2) |
где a и b – произвольные, отличные от нуля числа, и преобразуем его:
 |
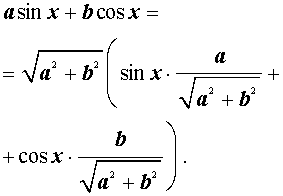(3) |
Введем дополнительный угол (вспомогательный аргумент) φ , у которого:
 |
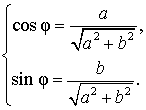(4) |
В случае, когда a и b являются положительными числами, в качестве дополнительного угла можно взять, например, угол
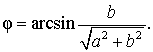
Тогда выражение (3) принимает вид:
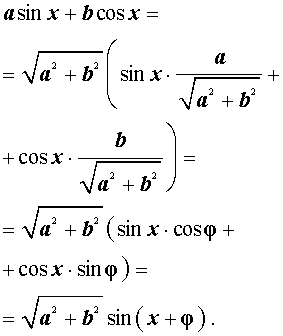
Таким образом, мы получили формулу
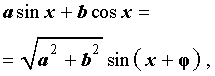
которую и называют формулой дополнительного угла (вспомогательного аргумента).
Если же дополнительный угол, в отличие от формул (4), ввести по формулам
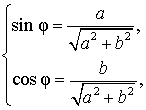
то выражение (3) примет вид
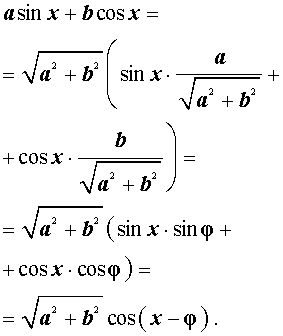
и мы получаем другой вид формулы дополнительного угла:
