Справочник по математикеТеория вероятностей и статистика Теория вероятностей

Операции над событиями. Диаграммы Эйлера – Венна

Содержание

	Произведение (пересечение) двух событий
	Сумма (объединение) двух событий
	Разность двух событий
	Симметрическая разность двух событий
	Переход к противоположному событию

В теории вероятностей случайными событиями являются подмножества множества элементарных исходов   Ω .  

Над событиями, как и над любыми множествами, можно совершать следующие операции.

Произведение (пересечение) двух событий

Операцию произведения (пересечения) двух событий   A   и   B  обозначают

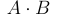,   или   AB,   или   .

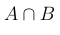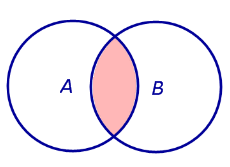
ОПРЕДЕЛЕНИЕ 1. Произведением (пересечением) двух событий   A   и   B   называют такое событие, которое состоит из всех элементов, входящих как в событие   A ,   так и в событие   B   (рис. 1).

Событие   A Событие   B Событие

Рис.1

Сумма (объединение) двух событий

Операцию суммы (объединения) двух событий   A   и   B  обозначают

A + B   или  

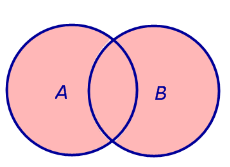
ОПРЕДЕЛЕНИЕ 2. Суммой (объединением) двух событий   A   и   B   называют такое событие, которое состоит из элементов события   A   и элементов события   B   (рис. 2).

Событие   A Событие   B Событие   A + B

Рис.2

Разность двух событий

Операцию разности двух событий   A   и   B  обозначают

A \ B

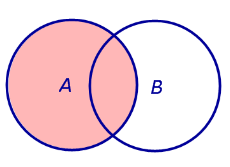
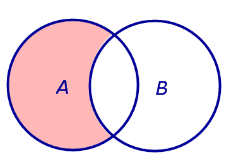
ОПРЕДЕЛЕНИЕ 3. Разностью событий   A   и   B   называют событие, состоящее из тех элементов события   A ,  которые не входят в событие   B   (рис. 3).

Событие   A Событие   B Событие   A \ B

Рис.3

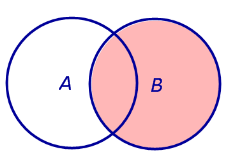
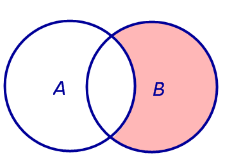
ЗАМЕЧАНИЕ 1. Разностью событий   B   и   A   является событие   B \ A ,   изображенное на рисунке 4.

Событие   A Событие   B Событие   B \ A

Рис.4

Симметрическая разность двух событий

Операцию симметрической разности двух событий   A   и   B  обозначают

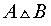
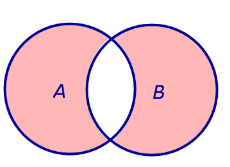
ОПРЕДЕЛЕНИЕ 4 . Симметрической разностью событий   A   и   B   называют событие, состоящее из тех элементов события   A ,  которые не входят в событие   B ,   а также из тех элементов события   B ,  которые не входят в событие   A   (рис. 5).

Событие   A Событие   B Событие

Рис.5

Переход к противоположному событию

Событие, противоположное к событию   A ,  обозначают

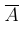  или   A^C

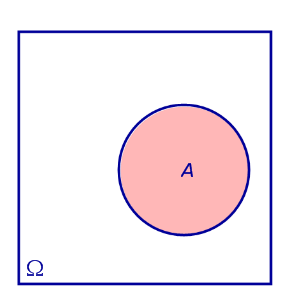
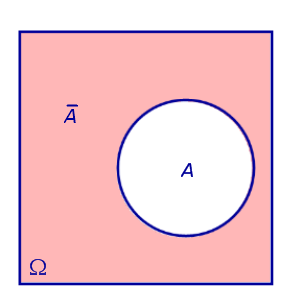
ОПРЕДЕЛЕНИЕ 5. Противоположным событием к событию   A   называют событие, состоящее из тех элементов всего множества элементарных событий   Ω ,   которые не входят в событие   A  (рис. 6).

Множество   Ω Событие   A Событие

Рис.6

ЗАМЕЧАНИЕ 2. Справедлива формула

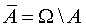
ОПРЕДЕЛЕНИЕ 6. Событие   Ω   называют достоверным событием, пустое множество 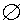    называют невозможным событием.

ЗАМЕЧАНИЕ 3. Рисунки, на которых наглядно показаны операции над множествами, называют диаграммами Эйлера-Венна. В частности, диаграммами Эйлера-Венна являются рисунки 1-6 .