Справочник по математике

Геометрия (Стереометрия)

Вписанные и описанные фигуры

Призмы, вписанные в цилиндры

Призмы, вписанные в цилиндр. Свойства призмы, вписанной в цилиндр

Отношение объема прямоугольного параллелепипеда к объему описанного около этого параллелепипеда цилиндра

Отношение объема правильной n - угольной призмы к объему описанного около этой призмы цилиндра

Призмы, вписанные в цилиндр. Свойства призмы, вписанной в цилиндр

      Определение 1. Призмой, вписанной в цилиндр, называют такую призму, основания которой вписаны в окружности оснований цилиндра, а боковые ребра призмы являются образующими цилиндра (рис. 1).

      Определение 2. Если призма вписана в цилиндр, то цилиндр называют описанным около призмы.

Рис.1

      Прежде, чем перейти к вопросу о том, какую призму можно вписать в цилиндр, докажем следующее свойство призм.

      Утверждение 1. Если около оснований призмы можно описать окружности, то отрезок, соединяющий центры описанных окружностей, будет параллелелен и равен боковому ребру призмы.

      Доказательство. Рассмотрим призму   A₁A₂ ... A_nA'₁A'₂ ... A'_n,   у которой около оснований
A₁A₂ ... A_n   и   A'₁A'₂ ... A'_n   можно описать окружности. Пусть около нижнего основания   A₁A₂ ... A_n   призмы   A₁A₂ ... A_nA'₁A'₂ ... A'_n   описана окружность с центром   O   радиуса   r.   Проведем через точку   O   прямую, параллельную боковому ребру   A₁A'₁   призмы и пересекающую плоскость верхнего основания в некоторой точке, которую обозначим   O'.

      Докажем, что точка   O'  является центром окружности радиуса   r,   описанной около верхнего основания призмы. С этой целью рассмотрим, например, четырехугольник   A₁A'₁O'O   (рис. 2).

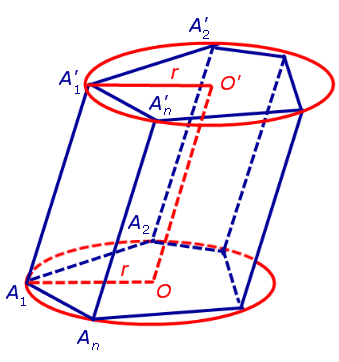
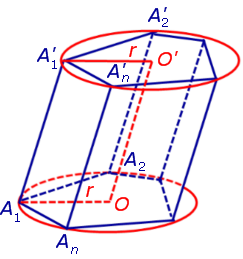
Рис.2

      Этот четырехугольник является параллелограммом, поскольку прямые   A₁A'₁   и   OO'   параллелельны по построению, а прямые   A₁O   и   A'₁O'   параллельны как линии пересечения двух параллельных плоскостей третьей плоскостью параллельны как линии пересечения двух параллельных плоскостей третьей плоскостью . Следовательно,

A'₁O' = A₁O = r .

      Рассуждая аналогичным образом, заключаем, что

A'₁O' = A'₂O' = ... =
= A'_nO' = r ,

то есть точка   O'   – центр окружности радиуса   r,   описанной около верхнего основания призмы.

      В силу того, что четырехугольник   OO'A₁A'₁   является параллелограммом, получаем равенство

OO' = A₁A'₁.

      Утверждение 1 доказано.

      Теорема. Около призмы можно описать цилиндр тогда и только тогда, когда выполнены следующие два условия:

1. Призма является прямой призмой;
2. Около оснований призмы можно описать окружности.

      Доказательство. Докажем сначала, что если около   n – угольной призмы описан цилиндр, то оба условия теоремы выполнены.

      Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, описанного около призмы. Из этого определения также следует, что вписанная в цилиндр призма является прямой призмой, поскольку образующие цилиндра перпендикулярны к плоскостям его оснований,

      Таким образом, мы доказали, что, если призма вписана в цилиндр, то оба условия теоремы выполнены.

      Теперь рассмотрим прямую n – угольную призму высоты   h,   около оснований которой можно описать окружности, и докажем, что около такой призмы можно описать цилиндр.

      Обозначим буквой   O   центр окружности радиуса   r,   описанной около нижнего основания призмы, а символом   O'   обозначим центр окружности, описанной около верхнего основания призмы.

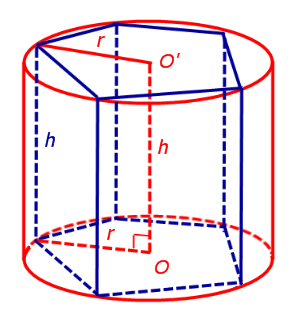
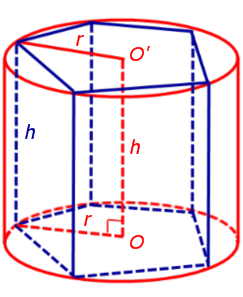
Рис.3

      Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы описанных около них окружностей будут равны. Согласно утверждению 1 отрезок   OO'   параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы   h.   Значит, и отрезок   OO'   перпендикулярен плоскости основания призмы и равен   h.

      Цилиндр с осью   OO',   радиусом   r   и высотой   h   и будет описан около исходной призмы.

      Доказательство теоремы завершено.

      Следствие 1. Высота призмы, вписанной в цилиндр, равна высоте цилиндра.

      Следствие 2. Около любой прямой треугольной призмы можно описать цилиндр (рис. 4).

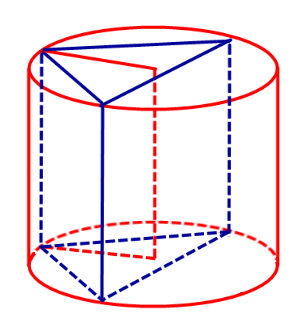
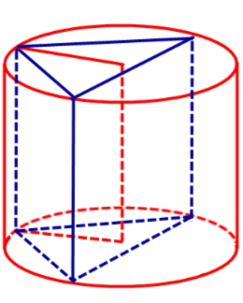
Рис.4

      Справедливость следствия 2 вытекает из того, что около любого треугольника можно описать окружность.

      Следствие 3. Около любого прямоугольного параллелепипеда (в частности, около куба прямоугольного параллелепипеда (в частности, около куба) можно описать цилиндр (рис. 5).

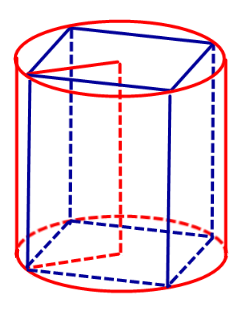
Рис.5

      Справедливость следствия 3 вытекает из того, что около любого прямоугольника можно описать окружность.

      Замечание 1. Если у прямоугольного параллелепипеда прямоугольного параллелепипеда три ребра, выходящие из одной вершины, равны  a, b, c  и различны, то существует три возможности описать около этого параллелепипеда цилиндр в зависимости от того, какое из ребер параллелепипеда выбрано в качестве образующей описанного цилиндра (рис. 6, 7, 8).

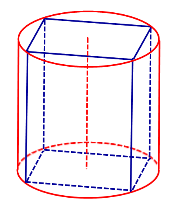Рис.6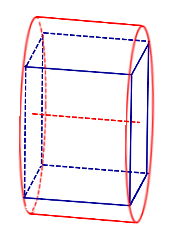

Рис.7

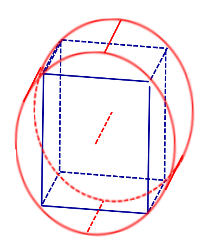
Рис.8

      Следствие 4 . Около любой правильной n - угольной призмы можно описать цилиндр (рис. 9).

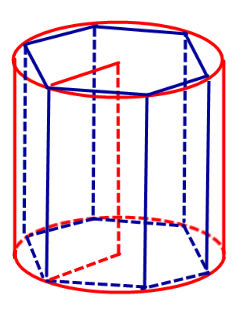
Рис.9

      Для доказательства следствия 4 достаточно заметить, что правильная n – угольная призма – это прямая призма, основания которой являются правильными n – угольниками, а около любого правильного n – угольника можно описать окружность.

Отношение объема прямоугольного параллелепипеда к объему описанного около него цилиндра

      Задача 1. Около прямоугольного параллелепипеда прямоугольного параллелепипеда с ребрами   a, b, c   описан цилиндр так, что высота цилиндра равна   c .   Найти отношение объемов призмы и цилиндра.

      Решение. Объем прямоугольного параллелепипеда Объем прямоугольного параллелепипеда   ABCDA'B'C'D'   (рис.10)

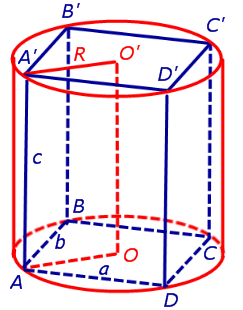
Рис.10

вычисляется по формуле

а объем цилиндра, описанного около этого параллелепипеда, можно найти по формуле

где   R – это радиус окружности, описанной около прямоугольника со сторонами   a   и   b   (рис 11).

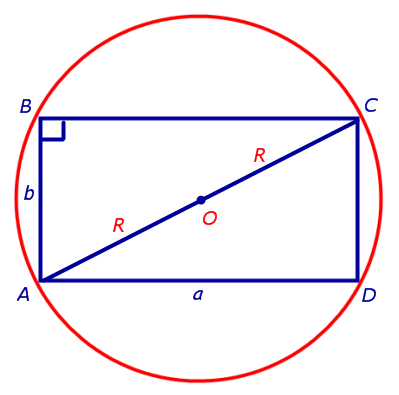
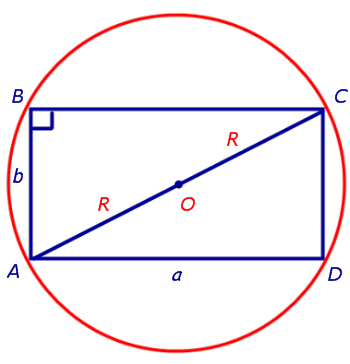
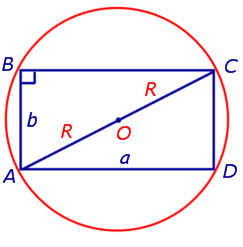
Рис.11

      Поскольку угол   ABC   прямой, то отрезок   AC   является диаметром окружности и равен   2R . По теореме Пифагора находим, что

4R² = a² + b² ,

      Следовательно,

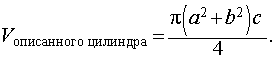
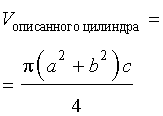
      Таким образом

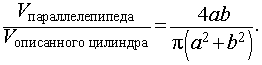
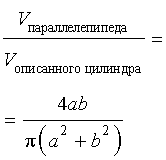
      Ответ.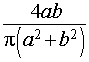

      Задача 2. Около куба куба с ребром   a   описан цилиндр. Найти отношение объемов куба и цилиндра.

      Решение. Поскольку куб является прямоугольным параллелепипедом, прямоугольным параллелепипедом, у которого все ребра равны, то, используя результат задачи 1, получаем

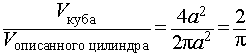
      Ответ.

Отношение объема правильной n - угольной призмы к объему описанного около этой призмы цилиндра

      Задача 3. Около правильной n - угольной призмы описан цилиндр. Найти отношение объемов призмы и цилиндра.

      Решение. Поскольку и объем призмы,объем призмы, и объем цилиндра вычисляются по формуле

V = S_осн h,

а высота призмы равна высоте описанного около нее цилиндра, то для объемов правильной n - угольной призмы и описанного около нее цилиндра справедливо равенство

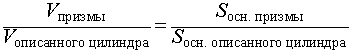
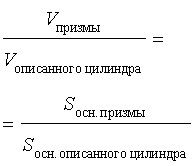
      С помощью формулы для площади правильного n - угольника, вписанного в окружность радиуса   R,   получаем, что

      Следовательно,

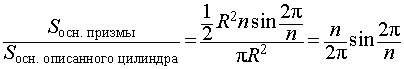
      Ответ.

      Следствие 5. Отношение объема правильной треугольной призмы правильной треугольной призмы к объему описанного около нее цилиндра равно

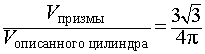
      Следствие 6. Отношение объема правильной четырехугольной призмы правильной четырехугольной призмы к объему описанного около нее цилиндра равно

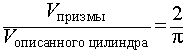
      Следствие 7. Отношение объема правильной шестиугольной призмы к объему описанного около нее цилиндра равно

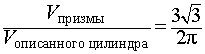
      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.