Справочник по математике

Геометрия (Стереометрия)

Вписанные и описанные фигуры

Сфера, описанная около конуса.
Отношение объемов конуса и описанной около него сферы

      Определение 1. Конусом, вписанным в сферу, называют такой конус, у которого вершина и окружность основания лежат на сфере (рис. 1).

      Определение 2. Если конус вписан в сферу, то сферу называют описанной около конуса.

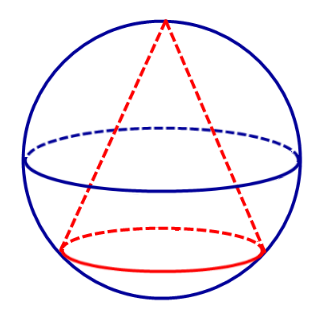
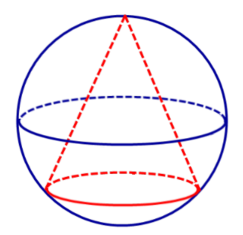
Рис.1

      Утверждение. Около любого конуса можно описать сферу, причем только одну. Центр описанной сферы лежит на оси конуса.

      Доказательство. Рассмотрим конус высоты   h,   в основании которого лежит круг радиуса   r  с центром в точке   O' .   Обозначим буквой   S   вершину конуса, а буквой   A   – произвольную точку на окружности основания конуса (рис. 2).

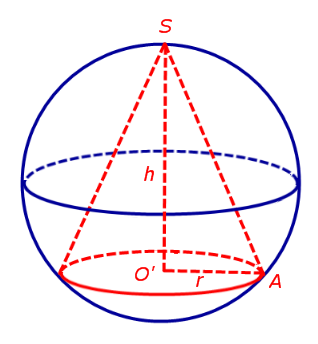
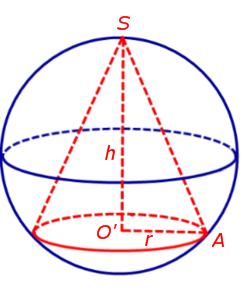
Рис.2

      Рассмотрим сечение конуса плоскостью   ASO'   и проведем серединный перпендикуляр к отрезку   SA .   Обозначим буквой   O   точку пересечения этого серединного перпендикуляра с прямой   SO'   и соединим точку   O   с точкой   A   (рис. 3).

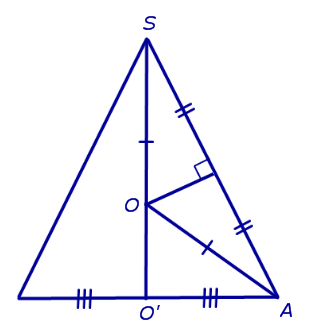
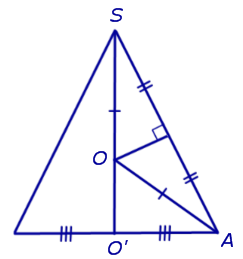
Рис.3

      По свойству серединного перпендикуляра точка   O   находится на одинаковом расстоянии от точек   A   и   S .   Обозначим это расстояние через   x   и покажем, что   x   не зависит от выбора точки   A   (рис. 4).

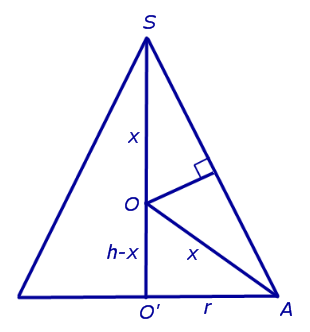
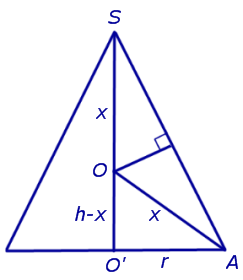
Рис.4

      Действительно, с помощью теоремы Пифагора из прямоугольного треугольника   AOO'   получим:

x² = (h – x )² + r² ,

x² = h² – 2hx + x² + r² ,

2hx = h² + r² .

      Следовательно,

      Таким образом, мы установили, что точка   O   находится на одном и том же расстоянии   x,   которое зависит лишь от высоты и радиуса основания конуса, от всех точек окружности основания конуса и от его вершины   S .   Значит, точка   O   – центр сферы, описанной около конуса.

      Для доказательства единственности описанной около конуса сферы заметим, что точка, равноудаленная от всех точек окружности основания конуса, должна лежать на перпендикуляре к плоскости основания конуса, проходящем через центр этой окружности. А точка, равноудаленная от вершины конуса и от какой-либо точки на окружности основания конуса, должна лежать на серединном перпендикуляре к образующей конуса, проходящей через эту точку. Таким образом, центром сферы, описанной около конуса, может быть лишь построенная выше точка   O .

      Следствие 1. Радиус сферы, описанной около конуса с радиусом основания   r   и высотой   h   равен

      Следствие 2. Отношение объема конуса к объему описанной около него сферы можно найти по формуле

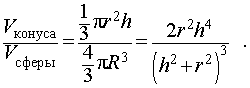
      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.