Справочник по математике

Геометрия (Стереометрия)

Вписанные и описанные фигуры

Конус, вписанный в цилиндр

Конус, вписанный в цилиндр

Отношение объемов конуса и описанного около него цилиндра

Конус, вписанный в цилиндр

      Определение 1. Конусом, вписанным в цилиндр, называют такой конус, у которого основание совпадает с одним из оснований цилиндра, а вершина совпадает с центром другого основания цилиндра (рис. 1).

      Определение 2. Если конус вписан в цилиндр, то цилиндр называют описанным около конуса.

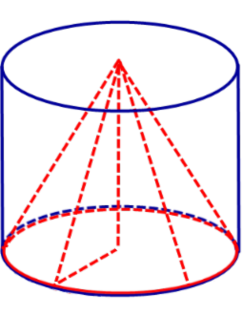
Рис.1

      Замечание. Высота конуса равна высоте цилиндра, описанного этого конуса.

      Утверждение. Около любого конуса можно описать цилиндр.

      Доказательство. Для доказательства достаточно построить цилиндр, у которого одно из оснований совпадает с основанием конуса, а плоскость другого основания проходит через вершину конуса.

Отношение объемов конуса и описанного около него цилиндра

      Утверждение. Объем конуса в 3 раза меньше объема описанного около него цилиндра.

      Доказательство. Пусть радиус основания конуса равен   r,   а высота конуса равна   h.   Поскольку цилиндр описан около конуса, то радиус основания цилиндра также равен   r,   а высота цилиндра равна   h.   Тогда объем конуса равен

,

а объем цилиндра равен

V _{описанного цилиндра} = πr²h.

      Таким образом,

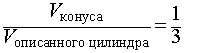
что и требовалось доказать.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.