Справочник по математике Тригонометрия
Тригонометрия
Свойства тригонометрических функций
Содержание
 |
Знаки тригонометрических функций |
 |
Периодичность тригонометрических функций |
 |
Четность тригонометрических функций |

Знаки тригонометрических функций
Знаки чисел
sin α , cos α , tg α , ctg α
определяются тем, в каком квадранте (четверти) координатной плоскости Oxy лежит луч OM (рисунки 1, 2, 3, 4).
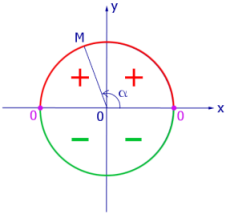
Рис.1. Знак sin α
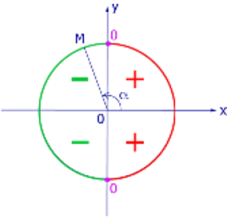
Рис.2. Знак cos α
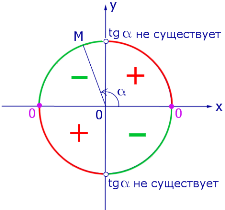
Рис.3. Знак tg α
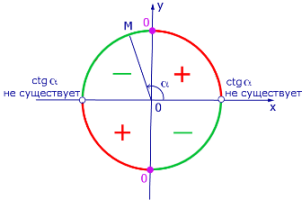
Рис.4. Знак ctg α
Периодичность тригонометрических функций. Полупериодичность синуса и косинуса
Рассмотрим рисунок 5.
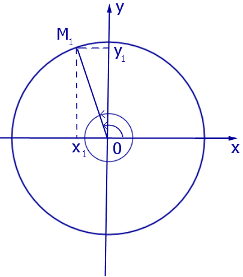
Рис.5
Если луч OM1, изображенный на рисунке 5, повернуть по ходу или против хода часов на полный угол (360 градусов или 2π радиан), то он совместится с самим собой. Следовательно, справедливы формулы:
sin (α° + 360°) = sin α°, cos (α° + 360°) = cos α°,
sin (α° – 360°) = sin α°, cos (α° – 360°) = cos α°,
а также формулы:
sin (α + 2π) = sin α , cos (α + 2π) = cos α ,
sin (α – 2π) = sin α, cos (α – 2π) = cos α .
Поворачивая луч OM1 на полный угол по ходу или против хода часов n раз ( 360n градусов или 2nπ радиан), получаем следующие формулы:
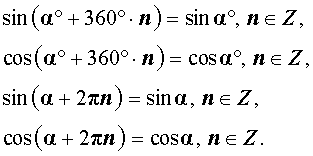
Таким образом, в случае, когда углы измеряются в градусах, периодами синуса и косинуса являются углы 360° n, 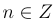 .
.
В случае, когда углы измеряются в радианах, периодами синуса и косинуса являются числа 2nπ, 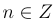 .
.
В случае, когда углы измеряются в градусах, наименьшим положительным периодом синуса и косинуса является угол 360°.
В случае, когда углы измеряются в радианах, наименьшим положительным периодом синуса и косинуса является число 2π .
Теперь рассмотрим рисунок 6.
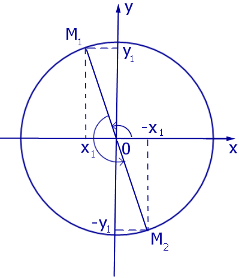
Рис.6
Если луч OM1, изображенный на рисунке 6, повернуть по ходу или против хода часов на развернутый угол (180 градусов или π радиан), то он совместится с лучом OM2 . Следовательно, справедливы формулы:
sin (α° + 180°) = – sin α°, cos (α° + 180°) = – cos α°,
sin (α° – 180°) = – sin α°, cos (α° – 180°) = – cos α°,
а также формулы:
sin (α + π) = – sin α , cos (α + π) = – cos α ,
sin (α – π) = – sin α, cos (α – π) = – cos α.
Полученные формулы описывают свойство полупериодичности синуса и косинуса.
Таким образом, в случае, когда углы измеряются в градусах, угол 180° является полупериодом синуса и косинуса.
В случае, когда углы измеряются в радианах, полупериодом синуса и косинуса является число π.
СЛЕДСТВИЕ. Поскольку
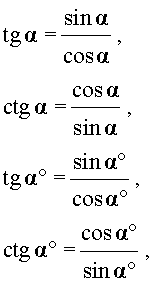
то справедливы формулы:
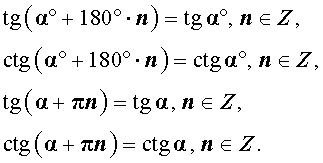
Таким образом, в случае, когда углы измеряются в градусах, периодами тангенса и котангенса являются углы 180° n, 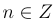
В случае, когда углы измеряются в радианах, периодами тангенса и котангенса являются числа nπ, 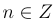 .
.
В случае, когда углы измеряются в градусах, наименьшим положительным периодом тангенса и котангенса является угол 180°.
В случае, когда углы измеряются в радианах, наименьшим положительным периодом тангенса и котангенса являются число π.
Четность тригонометрических функций
Рассмотрим рисунок 7.
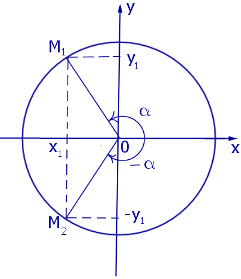
Рис.7
На этом рисунке
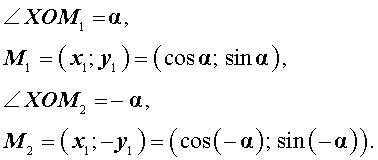
Следовательно, справедливы формулы:
sin ( – α ) = – sin α , cos ( – α ) = cos α ,
откуда вытекают формулы:
tg ( – α ) = – tg α , ctg ( – α ) = – ctg α .
Таким образом, косинус – четная функция, а синус, тангенс и котангенс – нечетные функции.
