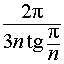Справочник по математике

Геометрия (Стереометрия)

Вписанные и описанные фигуры

Сфера, вписанная в призму

Сфера, вписанная в призму. Свойства прямой призмы, описанной около сферы

Отношение объемов шара и куба, описанного около сферы, ограничивающей этот шар

Свойства правильной призмы, описанной около сферы. Отношение объемов шара и правильной n - угольной призмы, описанной около сферы, ограничивающей этот шар

Сфера, вписанная в призму. Свойства прямой призмы, описанной около сферы

      Определение 1. Сферой, вписанной в призму, называют такую сферу, которая касается плоскостей всех граней призмы, причем точки касания лежат на гранях призмы (рис. 1).

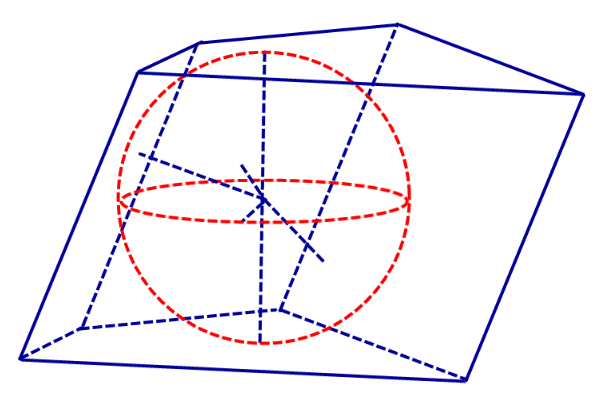
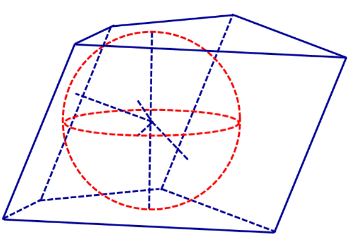
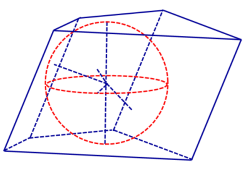
Рис.1

      Определение 2. Если сфера вписана в призму, то призму называют описанной около сферы.

      Таким образом, если призма описана около сферы, то плоскости всех граней призмы являются касательными плоскостями к этой сфере.

      Далее мы будем рассматривать только прямые призмы.

      Утверждение. Если в прямую призму вписана сфера радиуса   R ,   то высота призмы равна   2R ,   а в основания призмы можно вписать окружности радиуса   R .

      Доказательство. Рассмотрим прямую призму, описанную около сферы (рис.2).

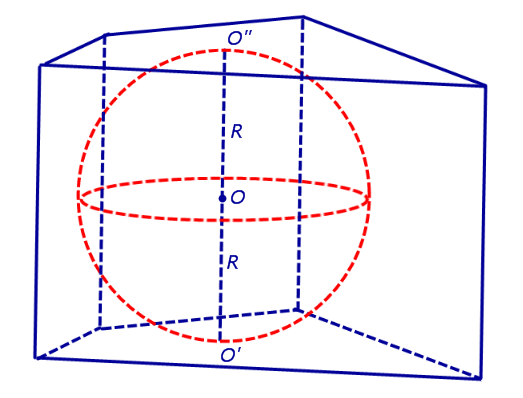
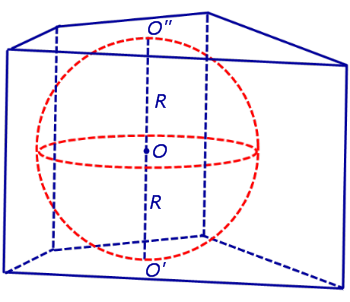
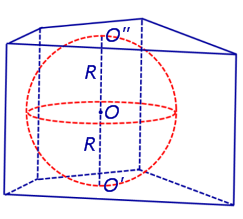
Рис.2

      Обозначим буквой   O   центр вписанной сферы, а символами   O'   и   O"   – точки касания сферы с плоскостями оснований призмы. Заметим, что плоскости оснований призмы параллельны, а радиусы   OO'   и   OO"   проведены в точки касания сферы с плоскостями оснований призмы и, следовательно, перпендикулярны плоскостям оснований призмы. Поэтому прямая   O'O"   перпендикулярна плоскостям оснований призмы, центр вписанной сферы   O   является серединой отрезка   O'O" ,   а высота призмы равна длине отрезка   O'O"   и равна   2R .

      Проведем через точку   O   плоскость, перпендикулярную прямой   O'O" ,   и докажем, что все точки касания сферы с боковыми гранями призмы лежат в этой плоскости. Для этого обозначим точку касания сферы с какой-либо гранью призмы буквой   L   и докажем, что прямая   OL   перпендикулярна прямой   O'O"   (рис. 3).

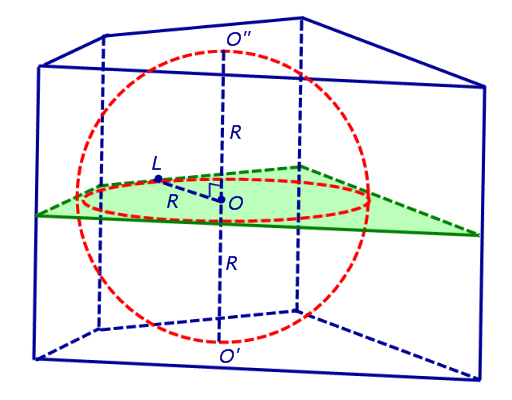
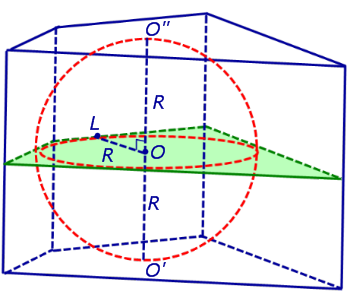
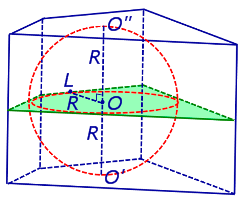
Рис.3

      Действительно, радиус   OL ,   проведенный в точку касания сферы с боковой гранью призмы перпендикулярен плоскости этой грани, а, значит, перпендикулярен любой прямой, лежащей на этой грани, и, в том числе,   OL   будет перпендикулярен боковому ребру призмы.

      Рассматриваемая призма является прямой призмой, поэтому ее боковые ребра перпендикулярны к плоскостям оснований. Прямая   O'O"   также перпендикулярна к плоскостям оснований и, следовательно, параллельна боковым ребрам призмы. следовательно, параллельна боковым ребрам призмы. Таким образом, мы можем заключить, что прямая   OL   перпендикулярна прямой   O'O"   и, значит, лежит в плоскости, перпендикулярной прямой   O'O"   и проходящей через точку  O .

      Сечение призмы и вписанной в нее сферы плоскостью, перпендикулярной прямой   O'O"   и проходящей через точку   O ,   представляет собой многоугольник, равный основаниям призмы, со вписанной в него окружностью радиуса   R   (рис. 3).

      Утверждение доказано.

      Следствие. В любой куб куб можно вписать сферу.

Отношение объемов шара и куба, описанного около сферы, ограничивающей этот шар

      Задача 1. Найти отношение объемов шара и куба, описанного около сферы, ограничивающей этот шар.

      Решение. Если сфера радиуса   R   вписана в куб, то ребро куба равно   2R   (рис. 4).

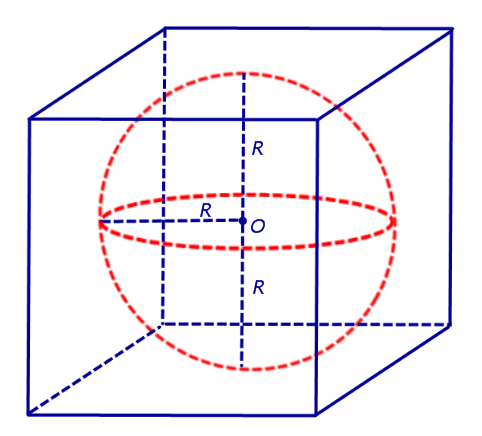
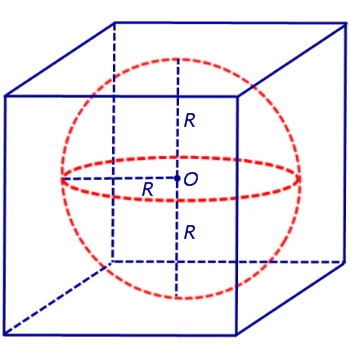
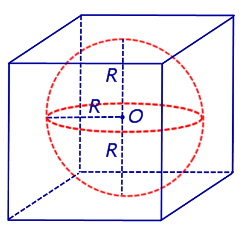
Рис.4

     Объем шара, ограниченного данной сферой, вычисляется по формуле

а объем куба с ребром   2R   вычисляется по формуле:

V_куба = (2R)³ = 8R³ .

      Следовательно,

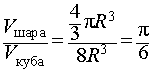(1)

      Ответ.

Свойства правильной призмы, описанной около сферы.
Отношение объемов шара и правильной n - угольной призмы,
описанной около сферы, ограничивающей этот шар

      Задача 2. В правильную n - угольную призму с ребром основания   a   вписана сфера. Найти:

1. Высоту призмы;
2. Отношение объемов шара, ограниченного вписанной в правильную n - угольную призму сферой, и призмы.

      Решение.

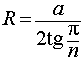
      Следовательно, высота призмы равна

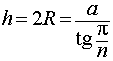
      Объем шара вычисляется по формуле

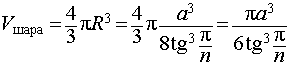
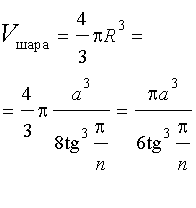
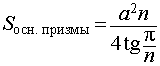
      Объем призмы находим по формуле:Объем призмы находим по формуле:

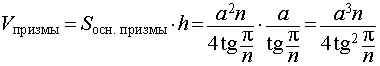
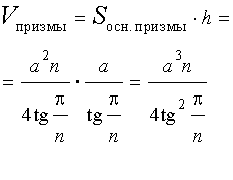
      Поэтому

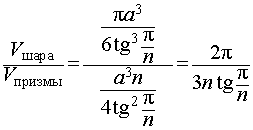
      Ответ.

      Следствие 1. Отношение объема шара к объему правильной треугольной призмы, правильной треугольной призмы, описанной около сферы, ограничивающей этот шар, равно

      Следствие 2. Отношение объема шара к объему правильной четырехугольной призмы, правильной четырехугольной призмы, описанной около сферы, ограничивающей этот шар, равно

      Замечание. Как мы видим, при   n = 4   формула для отношения объемов в ответе (пункт 2) совпадает с формулой (1).

      Следствие 3. Отношение объема шара к объему правильной шестиугольной призмы, описанной около сферы, ограничивающей этот шар, равно

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.