(495) 509-28-10КУРСЫ ЕГЭ и ОГЭМатематикаРусский язык + сочинениеСкоро начало занятий! |
 |
традиционно высокое качество преподавания; |
 |
индивидуальный подход к каждому; |
 |
маленькие группы; |
 |
бесплатное тестирование уровня знаний; |
 |
оплата производится ежемесячно; |
|
занятия, пропущенные по уважительной причине (болезнь, каникулы, отъезд и т.д.), не оплачиваются. |
Звоните и записывайтесь!
Занятия будут проходить 1 раз в неделю по 90 минут
Подробности по телефону (495) 509-28-10
Нам не все равно, как Вы сдадите экзамены!
А Вам?
|
|
||
|
|
Фигуры, составляющие основу планиметрии
Фигурой называют произвольное множество точек.
Планиметрия изучает свойства плоских фигур.
Углы, многоугольники, круги и другие, изучаемые в планиметрии фигуры, получены из основных фигур, составляющих Таблицу 1.
Таблица 1 – Основные планиметрические фигуры
| Рисунок фигуры | Название фигуры |
 | Точка |
 | Прямая |
 | Луч (полупрямая) |
 | Отрезок |
 | Плоскость |
 | Окружность |
 | Дуга окружности |
Точка |
Прямая |
Луч (полупрямая) |
Отрезок |
Плоскость |
Окружность |
Дуга окружности |
Таблица 2 – Взаимное расположение основных планиметрических фигур
Рисунок фигуры | Описание фигуры | |
 | Точка делит прямую на два луча | |
 | Через две различные точки проходит только одна прямая | |
 | Пересекающиеся прямые | Других случаев взаимного расположения двух различных прямых на плоскости не бывает |
 | Параллельные прямые | |
 | Через точку, не лежащую на прямой, проходит только одна параллельная прямая | |
 | Прямая делит плоскость на две полуплоскости и является общей границей этих полуплоскостей | |
 | Отрезок, соединяющий точки, лежащие в одной полуплоскости, не пересекается с границей полуплоскости | |
 | Отрезок, соединяющий точки, лежащие в разных полуплоскостях, пересекается с прямой, разделяющей полуплоскости | |
 | Одна из окружностей находится внутри другой окружности (окружности не пересекаются) | Других случаев взаимного расположения двух окружностей на плоскости не бывает |
 | Каждая из кружностей находится во внешней области для другой окружности (окружности не пересекаются) | |
 | Окружности пересекаются в двух точках | |
 | Окружности имеют только одну общую точку (внутреннее касание) | |
 | Окружности имеют только одну общую точку (внешнее касание) | |
 | Прямая пересекает окружность в двух точках | Других случаев взаимного расположения прямой и окружности на плоскости не бывает |
 | Прямая имеет только одну общую точку с окружностью (прямая и окружность касаются) | |
 | Прямая не пересекается с окружностью | |
| Точка, лежащая на прямой |
Точка делит прямую на два луча |
| Две точки и прямая |
Через две различные точки проходит только одна прямая |
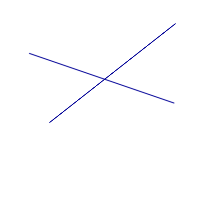
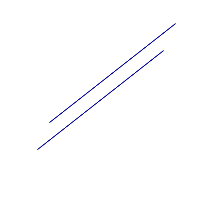
| Две прямые |
Пересекающиеся прямые |
Параллельные прямые |
Других случаев взаимного расположения двух различных прямых на плоскости не бывает |
| Точка, не лежащая на прямой |
Через точку, не лежащую на прямой, проходит только одна параллельная прямая |
| Прямая на плоскости |
Прямая делит плоскость на две полуплоскости и является общей границей этих полуплоскостей |
| Отрезок и прямая |
Отрезок, соединяющий точки, лежащие в одной полуплоскости, не пересекается с границей полуплоскости |
Отрезок, соединяющий точки, лежащие в разных полуплоскостях, пересекается с прямой, разделяющей полуплоскости |
| Две окружности |
Одна из окружностей находится внутри другой окружности (окружности не пересекаются) |
Каждая из кружностей находится во внешней области для другой окружности (окружности не пересекаются) |
Окружности пересекаются в двух точках |
Окружности имеют только одну общую точку (внутреннее касание) |
Окружности имеют только одну общую точку |
Других случаев взаимного расположения двух окружностей на плоскости не бывает |
| Прямая и окружность |
Прямая пересекает окружность в двух точках |
Прямая имеет только одну общую точку с окружностью (прямая и окружность касаются) |
Прямая не пересекается с окружностью |
| Других случаев взаимного расположения прямой и окружности на плоскости не бывает |
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
 подготовительные курсы для школьников 8, 9, 10 и 11 классов |
У нас также для школьников организованы
 индивидуальные занятия с репетиторами по математике и русскому языку |
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
