Числа Фибоначчи
 Определение последовательности Фибоначчи Определение последовательности Фибоначчи |
 Вывод формулы для общего члена последовательности Фибоначччи Вывод формулы для общего члена последовательности Фибоначччи |
Определение чисел Фибоначчи
Последовательностью (числами) Фибоначчи называют возвратную последовательность 2-го порядка, определяемую рекуррентной формулой
| xn = xn – 1 + xn – 2 , n > 2 | (1) |
с начальными условиями
| x1 = 1, x2 = 1 . | (2) |
Другими словами, последовательность Фибоначчи - это такая последовательность, у которой первые два члена равны 1, а каждый член, начиная с третьего члена, равен сумме двух предыдущих членов.
Таким образом, числа
1, 1, 2, 3, 5, 8, 13, 21, 34, 55
являются первыми десятью членами последовательности Фибоначчи.
Замечание. Определения возвратной последовательности, рекуррентной формулы, характеристического уравнения и формулы для общего решения рекуррентных уравнений приведены в разделе «Возвратные последовательности: рекуррентная формула, характеристическое уравнение» нашего справочника.
Вывод формулы общего члена последовательности Фибоначчи
Нашей целью является вывод формулы общего члена последовательности Фибоначчи. Чтобы получить эту формулу, будем действовать в соответствии со схемой, изложенной в разделе «Возвратные последовательности: вывод формулы общего члена».
Характеристическое уравнение для последовательности (1) имеет вид
λ2 – λ – 1 = 0 .
Найдем его корни:
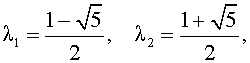
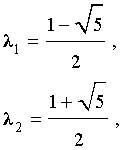
Поскольку корни характеристического уравнения вещественные и различные, то общее решение рекуррентного уравнения (1) имеет вид
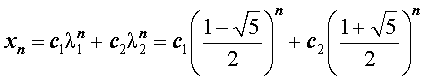
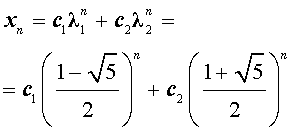
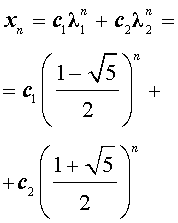
где c1 и c2 – произвольные действительные числа.
Найдем теперь значения произвольных постоянных c1 и c2 так, чтобы для последовательности
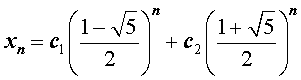
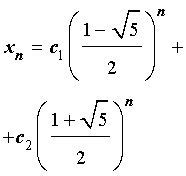
(3) выполнялись начальные условия (2). Это означает, что числа c1 и c2 должны удовлетворять следующей системе из двух линейных уравнений с двумя неизвестными:
- Решение этой системы имеет вид:Решим полученную систему уравнений:
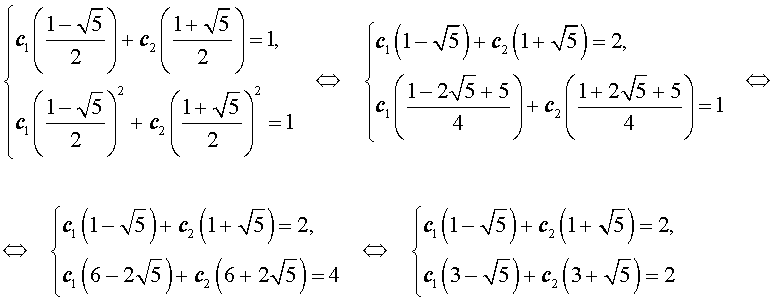
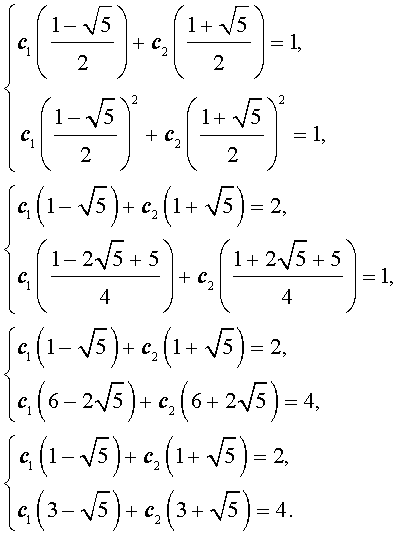
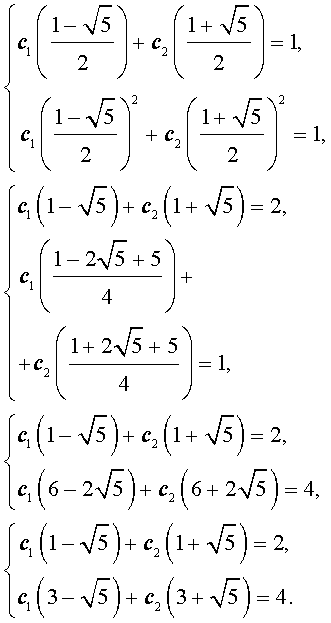
Для того, чтобы решить последнюю систему, вычтем первое уравнение из второго уравнения, оставив первое уравнение без изменений:
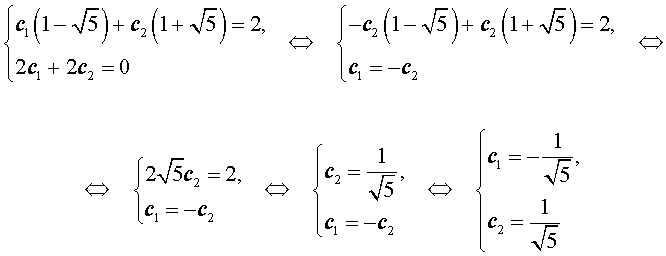
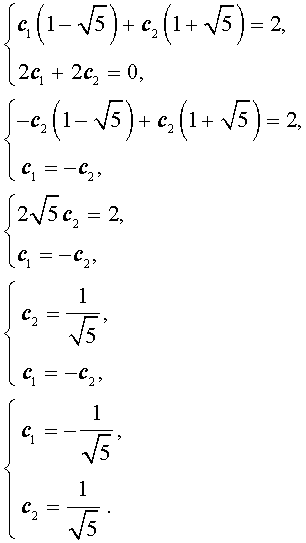
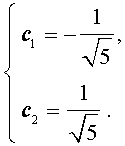
Посмотреть, как получено это решение можно, включив эту страницу на стационарном компьютере или планшете.
Подставляя найденные значения произвольных постоянных c1 и c2 в формулу (3), получаем искомую формулу общего члена последовательности Фибоначчи:
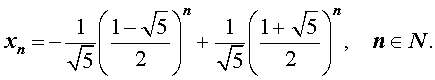
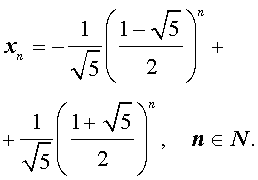
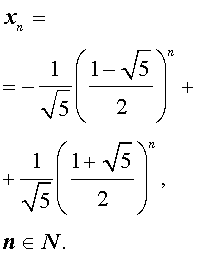
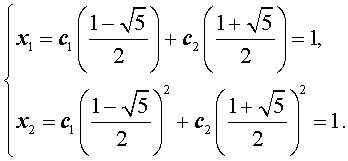
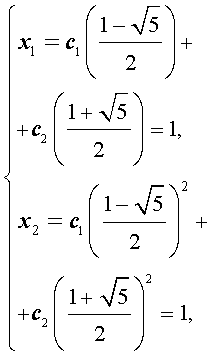
Замечание. Число
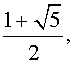
входящее в формулу общего члена последовательности Фибоначчи, является золотым отношением.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
|
