Элементарные преобразования графиков функций
Элементарные преобразования графика функции y = f (x ) перечислены в следующей таблице.
| Преобразование | Описание | Рисунок |
y = f (x + c), | В случае c > 0 график функции | 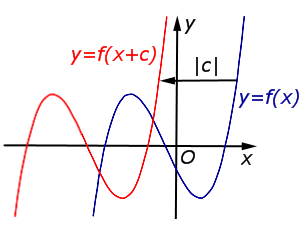 |
В случае c < 0 график функции | 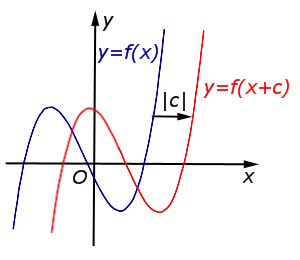 | |
y = f (x) + c, | В случае c > 0 график функции | 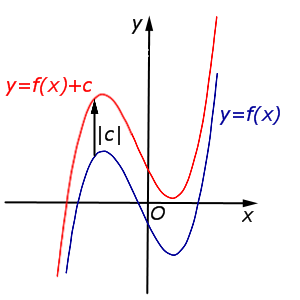 |
В случае c < 0 график функции | 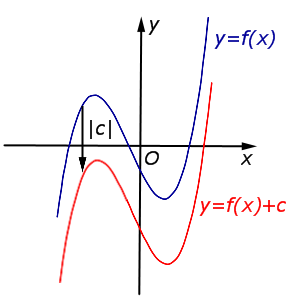 | |
| y = – f (x) | График функции y = f (x) симметрично отражается относительно оси Ox. | 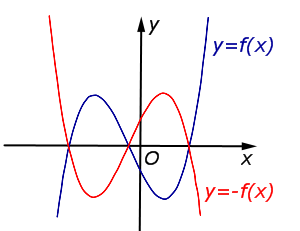 |
| y = f ( – x) | График функции y = f (x) симметрично отражается относительно оси Oy. | 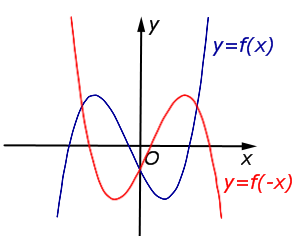 |
| В случае k > 1 происходит | 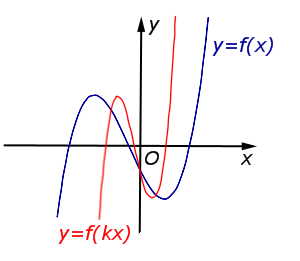 |
В случае 0 < k < 1 происходит растяжение графика функции | 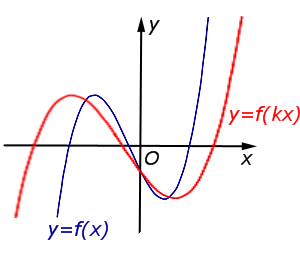 | |
В случае – 1 < k < 0 происходит растяжение графика функции | 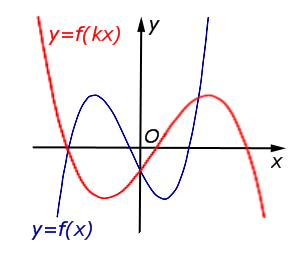 | |
В случае k < – 1 происходит | 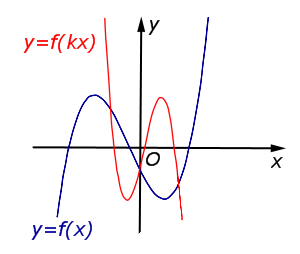 | |
| В случае k > 1 происходит | 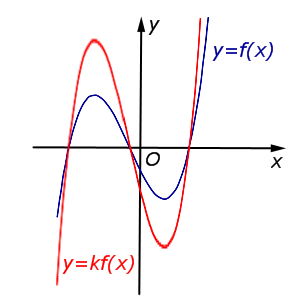 |
В случае 0 < k < 1 происходит | 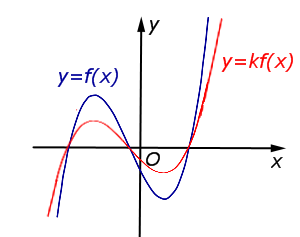 | |
В случае – 1 < k < 0 происходит | 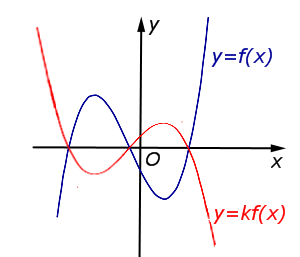 | |
В случае k < – 1 происходит | 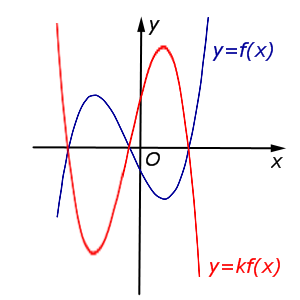 | |
| y = | f (x)| | Часть графика функции y = f (x), расположенная в области | 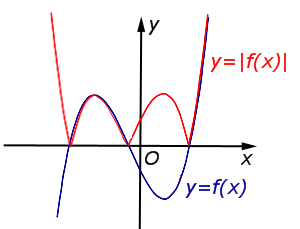 |
| y = f (| x|) | Ось Oy является осью симметрии Часть графика функции y = f (x), расположенная в области | 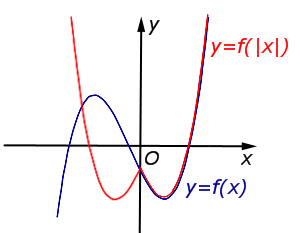 |
| Преобразование y = f (x + c), где c – число | |
В случае c > 0 график функции y = f (x) переносится влево на расстояние | c | |  |
В случае c < 0 график функции y = f (x) переносится вправо на расстояние | c | |  |
| Преобразование y = f (x) + c, где c – число | |
В случае c > 0 график функции y = f (x) переносится вверх на расстояние | c | |  |
В случае c < 0 график функции y = f (x) переносится вниз на расстояние | c | |  |
| Преобразование y = – f (x) | |
График функции y = f (x) симметрично отражается относительно оси Ox. |  |
| Преобразование y = f ( – x) | |
График функции y = f (x) симметрично отражается относительно оси Oy. |  |
| Преобразование y = f (kx), где k – число | |
В случае k > 1 происходит сжатие графика функции |  |
В случае 0 < k < 1 происходит растяжение графика функции y = f (x) в |  |
В случае – 1 < k < 0 происходит растяжение графика функции y = f (x) в |  |
В случае k < – 1 происходит сжатие графика функции |  |
| Преобразование y = k f (x), где k – число | |
В случае k > 1 происходит растяжение графика функции y = f (x) в k раз от оси Ox. |  |
В случае 0 < k < 1 происходит сжатие графика функции y = f (x) в |  |
В случае – 1 < k < 0 происходит сжатие графика функции y = f (x) в |  |
В случае k < – 1 происходит растяжение графика функции y = f (x) в | k | раз от оси Ox с последующим симметричным отражением графика относительно оси Ox. |  |
| Преобразование y = | f (x)| | |
Часть графика функции | 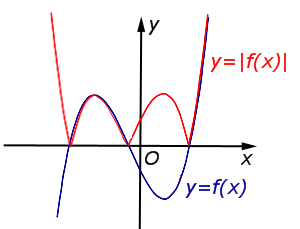 |
| Преобразование y = f (| x|) | |
Ось Oy является осью симметрии графика функции y = f (| x|). Часть графика функции |  |
| Преобразование y = f (x + c), где c – число |
Описание: В случае c > 0 график функции y = f (x) переносится влево на расстояние | c | Рисунок:  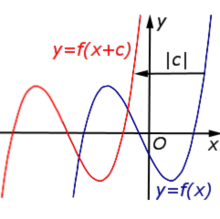 |
Описание: В случае c < 0 график функции y = f (x) переносится вправо на расстояние | c | Рисунок:  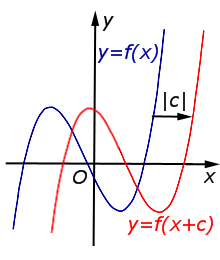 |
| Преобразование y = f (x) + c, где c – число |
Описание: В случае c > 0 график функции y = f (x) переносится вверх на расстояние | c | Рисунок:  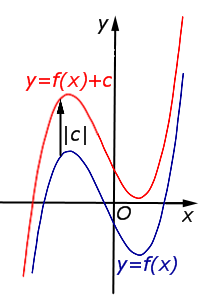 |
Описание: В случае c < 0 график функции y = f (x) переносится вниз на расстояние | c | Рисунок:  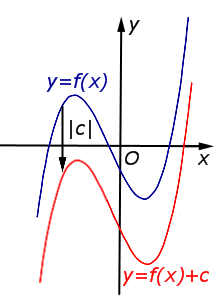 |
| Преобразование y = – f (x) |
Описание: График функции y = f (x) симметрично отражается относительно оси Ox. Рисунок:  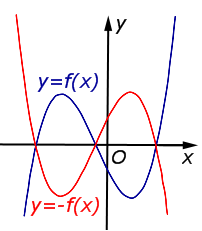 |
| Преобразование y = f ( – x) |
Описание: График функции y = f (x) симметрично отражается относительно оси Oy. Рисунок:  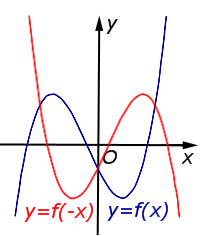 |
| Преобразование y = f (kx), где k – число |
Описание: В случае k > 1 происходит сжатие графика функции y = f (x) в k раз к оси Oy. Рисунок:  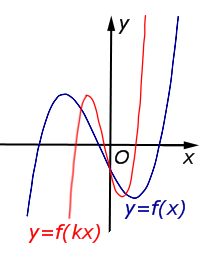 |
Описание: В случае 0 < k < 1 происходит растяжение графика функции y = f (x) в Рисунок:  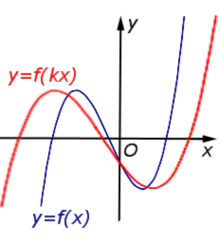 |
Описание: В случае – 1 < k < 0 происходит растяжение графика функции y = f (x) в Рисунок:  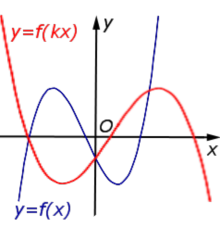 |
Описание: В случае k < – 1 происходит сжатие графика функции y = f (x) в | k | раз к оси Oy с последующим симметричным отражением графика относительно оси Oy. Рисунок:  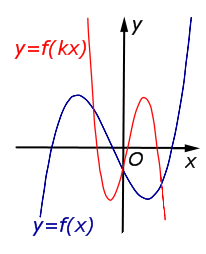 |
| Преобразование y = k f (x), где k – число |
Описание: В случае k > 1 происходит растяжение графика функции y = f (x) в k раз от оси Ox. Рисунок:  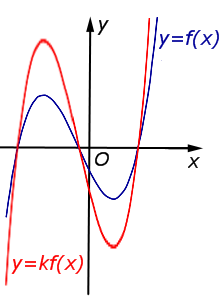 |
Описание: В случае 0 < k < 1 происходит сжатие графика функции y = f (x) в Рисунок:  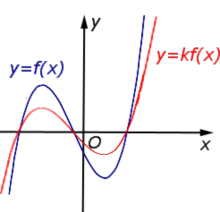 |
Описание: В случае – 1 < k < 0 происходит сжатие графика функции y = f (x) в Рисунок:  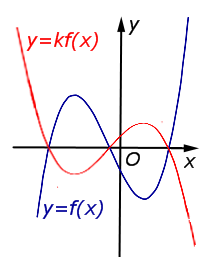 |
Описание: В случае k < – 1 происходит растяжение графика функции y = f (x) в | k | раз от оси Ox с последующим симметричным отражением графика относительно оси Ox. Рисунок:  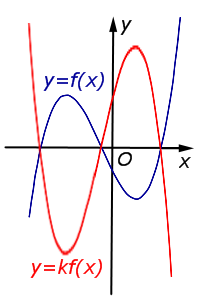 |
| Преобразование y = | f (x)| |
Описание: Часть графика функции y = f (x), расположенная в области Рисунок: 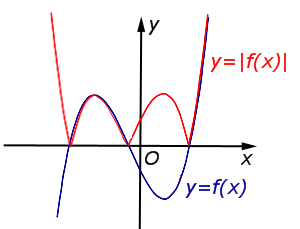 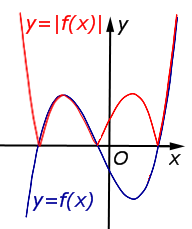 |
| Преобразование y = f (| x|) |
Описание: Ось Oy является осью симметрии графика функции y = f (| x|). Часть графика функции y = f (x), расположенная в области Рисунок:   |
Примеры элементарных преобразований графика функции y = x2 приведены в следующей таблице.
| Функция | График |
| y = x2 = f (x) | 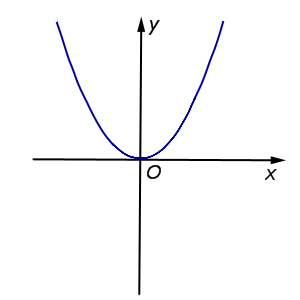 |
y = x2 + 4x + 4 = (x + 2)2 = = f (x + 2) | 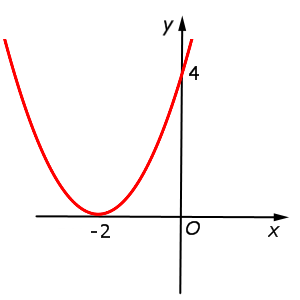 |
y = x2 – 4x + 4 = (x – 2)2 = = f (x – 2) | 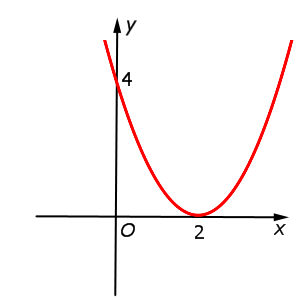 |
| y = x2 + 2 = f (x)+ 2 | 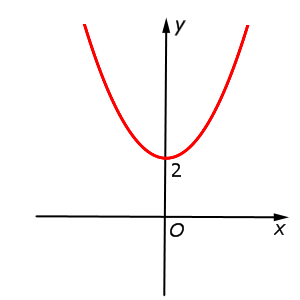 |
| y = x2 – 2 = f (x) – 2 | 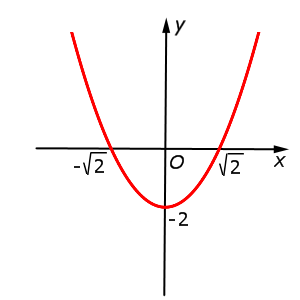 |
| y = – x2 = – f (x) | 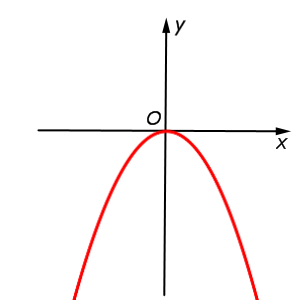 |
| y = 2x2 = 2 f (x) | 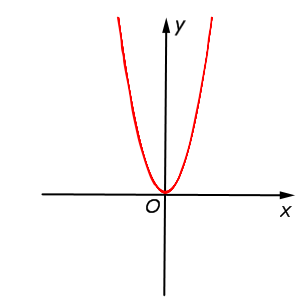 |
Функция: y = x2 = f (x) График:  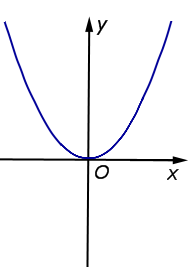 |
Функция: y = x2 + 4x + 4 = График:  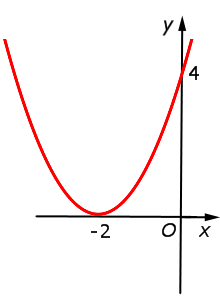 |
Функция: y = x2 – 4x + 4 = График:  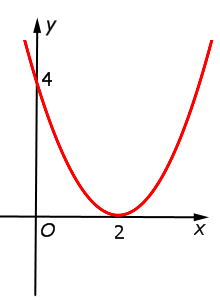 |
Функция: y = x2 + 2 = График:  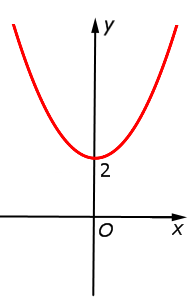 |
Функция: y = x2 – 2 = График:   |
Функция: y = – x2 = График:  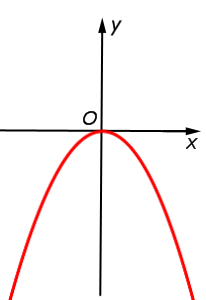 |
Функция: y = 2x2 = График:  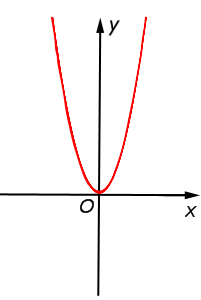 |
Примеры элементарных преобразований графика функции y = x2 – 6 x + 5 приведены в следующей таблице.
| Функция | График |
| y = x2 – 6x + 5 = = f (x) | 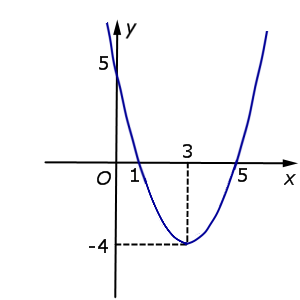 |
| y = x2 + 6x + 5 = = f (– x) | 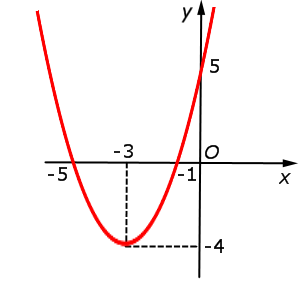 |
| y = 4x2 – 12x + 5 = = f (2x) | 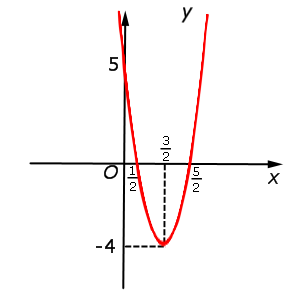 |
| y = | x2 – 6x + 5| = = | f (x)| | 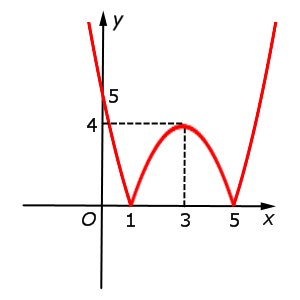 |
| y = x2 – 6 | x| + 5 = = f (| x|) | 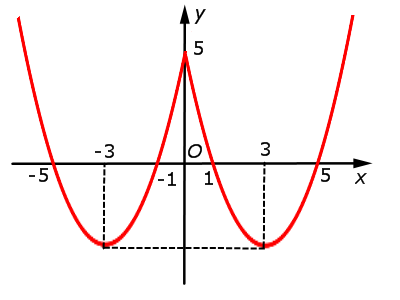 |
Функция: y = x2 – 6x + 5 = График:  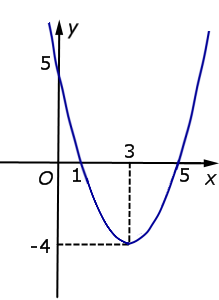 |
Функция: y = x2 + 6x + 5 = График:  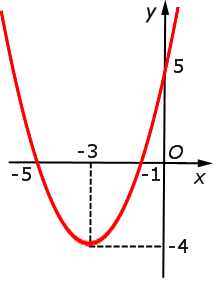 |
Функция: y = 4x2 – 12x + 5 = График:  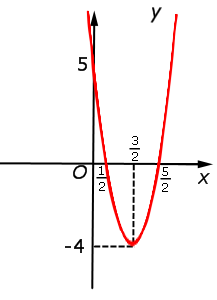 |
Функция: y = | x2 – 6x + 5| = График:  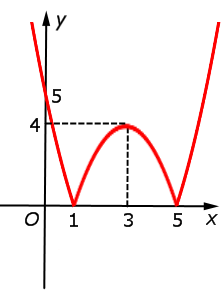 |
Функция: y = x2 – 6 | x| + 5 = График:  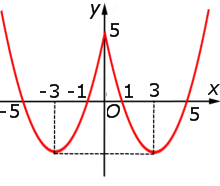 |

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
