Справочник по математике Геометрия (Планиметрия)
Геометрия (Планиметрия) Окружность и круг
Окружность и круг
Площадь круга и его частей. Длина окружности и ее дуг
Содержание
 |
Основные определения и свойства. Число π |
 |
Формулы для площади круга и его частей |
 |
Формулы для длины окружности и ее дуг |
 |
Площадь круга |
 |
Длина окружности |
 |
Длина дуги |
 |
Площадь сектора |
 |
Площадь сегмента |

Основные определения и свойства
| Определение окружности |
|
Определение Окружностью называют множество точек плоскости, находящихся на одном и том же расстоянии от одной точки - центра окружности |
| Определение дуги окружности |
|
Определение Дугой называют часть окружности, расположенную между двумя точками окружности |
| Определение круга |
|
Определение Кругом называют конечную часть плоскости, ограниченную окружностью |
| Определение сектора |
|
Определение |
| Определение сегмента |
|
Определение Сегментом называют часть круга, ограниченную хордой |
| Определение правильного многоугольника |
|
Определение Правильным многоугольником называют выпуклый многоугольник, у которого все стороны равны и все углы равны |
| Свойство правильного многоугольника |
|
Свойство Около любого правильного многоугольника можно описать окружность |
ОПРЕДЕЛЕНИЕ 1. Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
ОПРЕДЕЛЕНИЕ 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
ЗАМЕЧАНИЕ 1. Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
ОПРЕДЕЛЕНИЕ 3. Числом π (пи) называют число, равное площади круга радиуса 1.
ЗАМЕЧАНИЕ 2. Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
| Формула для площади круга |
|
|
| Формула для площади сектора с углом в радианах |
|
Здесь величина угла α выражена радианах |
| Формула для площади сектора с углом в градусах |
|
Здесь величина угла α выражена в градусах |
| Формула для площади сегмента с углом в радианах |
|
Здесь величина угла α выражена в радианах |
| Формула для площади сегмента с углом в градусах |
|
Здесь величина угла α выражена в градусах |
Формулы для длины окружности и её дуг
| Формула для длины окружности |
|
|
| Формула для длины дуги окружности, заданной углом в радианах |
|
Здесь величина угла α выражена в радианах |
| Формула для длины дуги окружности, заданной углом в градусах |
|
Здесь величина угла α выражена в градусах |
Площадь круга
Рассмотрим две окружности с общим центром (концентрические окружности) и радиусами 1 и R, в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1.

Рис.1
Площадь правильного n – угольника, вписанного в окружность радиуса R, равна

Площадь правильного n – угольника, вписанного в окружность радиуса 1, равна

Следовательно,

Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1, стремится к π, то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R, стремится к числу πR2.
Таким образом, площадь круга радиуса R, обозначаемая S, равна
S = πR2.
Длина окружности
Рассмотрим правильный n – угольник B1B2…Bn , вписанный в окружность радиуса R, и опустим из центра O окружности перпендикуляры на все стороны многоугольника (рис. 2).

Рис.2
Поскольку площадь n – угольника B1B2…Bn равна

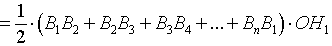
то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R:
C = 2πR.
СЛЕДСТВИЕ. Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

Рис.3
В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

Рис.4
В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Рис.5
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем

Следовательно,

В случае, когда величина α выражена в в радианах, получаем
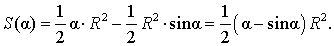
Следовательно,