Справочник по математике

Геометрия (Планиметрия)

Треугольники

Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов

Серединный перпендикуляр к отрезку

Окружность описанная около треугольника

Свойства описанной около треугольника окружности. Теорема синусов

Доказательства теорем о свойствах описанной около треугольника окружности

Серединный перпендикуляр к отрезку

      Определение 1. Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

Рис.1

      Теорема 1. Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.

      Доказательство. Рассмотрим произвольную точку   D,   лежащую на серединном перпендикуляре к отрезку   AB   (рис.2), и докажем, что треугольники   ADC   и   BDC   равны.

Рис.2

      Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты   AC   и   BC   равны, а катет   DC   является общим. Из равенства треугольников   ADC   и   BDC   вытекает равенство отрезков   AD   и   DB.   Теорема 1 доказана.

      Теорема 2 (Обратная  к теореме 1). Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

      Доказательство. Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка   E   находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки   E   и   A   лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок   EA   пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой   D.

Рис.3

      Докажем, что отрезок   AE   длиннее отрезка   EB.   Действительно,

      Таким образом, в случае, когда точки   E   и   A   лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Рис.4

      Теперь рассмотрим случай, когда точки   E   и   A   лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок   EB   длиннее отрезка   AE.   Действительно,

      Полученное противоречие и завершает доказательство теоремы 2

Окружность, описанная около треугольника

      Определение 2. Окружностью, описанной около треугольника, называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником.

Рис.5

Свойства описанной около треугольника окружности. Теорема синусов

Фигура	Рисунок	Свойство
Серединные перпендикуляры к сторонам треугольника		Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство
Окружность, описанная около треугольника		Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство
Центр описанной около остроугольного треугольника окружности		Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружности		Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство
Центр описанной около тупоугольного треугольника окружности		Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теорема синусов		Для любого треугольника справедливы равенства (теорема синусов): , где   a , b , c   – стороны треугольника,   A , B , С   – углы треугольника,   R   – радиус описанной окружности. Посмотреть доказательство
Площадь треугольника		Для любого треугольника справедливо равенство: S = 2R2 sin A sin B sin C , где   A , B , С   – углы треугольника,   S   – площадь треугольника,   R   – радиус описанной окружности. Посмотреть доказательство
Радиус описанной окружности		Для любого треугольника справедливо равенство: где   a , b , c   – стороны треугольника,   S   – площадь треугольника,   R   – радиус описанной окружности. Посмотреть доказательство

Серединные перпендикуляры к сторонам треугольника

Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство

Окружность, описанная около треугольника

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство

Центр описанной около остроугольного треугольника окружности

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центр описанной около прямоугольного треугольника окружности

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство

Центр описанной около тупоугольного треугольника окружности

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов): , где   a , b , c   – стороны треугольника,   A , B , С   – углы треугольника,   R   – радиус описанной окружности. Посмотреть доказательство

Площадь треугольника

Для любого треугольника справедливо равенство: S = 2R2 sin A sin B sin C , где   A , B , С   – углы треугольника,   S   – площадь треугольника,   R   – радиус описанной окружности. Посмотреть доказательство

Радиус описанной окружности

Для любого треугольника справедливо равенство: где   a , b , c   – стороны треугольника,   S   – площадь треугольника,   R   – радиус описанной окружности. Посмотреть доказательство

Доказательства теорем о свойствах описанной около треугольника окружности

      Теорема 3. Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

      Доказательство. Рассмотрим два серединных перпендикуляра, проведённых к сторонам   AC   и   AB   треугольника   ABC,   и обозначим точку их пересечения буквой   O   (рис. 6).

Рис.6

      Поскольку точка   O   лежит на серединном перпендикуляре к отрезку   AC,   то в силу теоремы 1 справедливо равенство:

CO = AO .

      Поскольку точка O лежит на серединном перпендикуляре к отрезку   AB,   то в силу теоремы 1 справедливо равенство:

AO = BO .

      Следовательно, справедливо равенство:

CO = BO ,

откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку   BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.

      Следствие. Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

      Доказательство. Рассмотрим точку   O,   в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника   ABC   (рис. 6).

      При доказательстве теоремы 3 было получено равенство:

AO = OB = OC ,

из которого вытекает, что окружность с центром в точке   O   и радиусами   OA,   OB,   OC   проходит через все три вершины треугольника   ABC,   что и требовалось доказать.

      Теорема 4 (теорема синусов). Для любого треугольника (рис. 7)

Рис.7

справедливы равенства:

.

      Доказательство. Докажем сначала, что длина хорды окружности радиуса   R хорды окружности радиуса   R,   на которую опирается вписанный угол величины   φ ,   вычисляется по формуле:

      Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).

Рис.8

      Угол   MPN,   как угол,опирающийся на диаметр, является прямым угломугол,опирающийся на диаметр, является прямым углом, и равенство (1) вытекает из определения синуса угла прямоугольного треугольника.

      Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.

      Формула (1) доказана.

      Из формулы (1) для вписанного треугольника   ABC   получаем (рис.7):

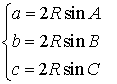
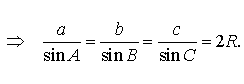
      Теорема синусов доказана.

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.